Euklidovský prostor. Euklides. Euklidovy postuláty (axiomy)
|
|
|
- Romana Dvořáková
- před 8 lety
- Počet zobrazení:
Transkript
1 Euklidovský prostor Euklidovy Základy (pohled do historie) dnešní definice kartézský souřadnicový systém vlastnosti rovin v E n speciální vlastnosti v E 3 (vektorový součin) a) eprostor, 16, b) P. Olšák, FEL ČVUT, c) P. Olšák 2010, d) BI-LIN, e) L, f) 2009/2010, g)ä. Viz p. d. 4/2010 [1] Euklides BI-LIN, eprostor, 16, P. Olšák [2] Euklides (jiný překlad: Eukleides) byl řecký matematik (kolem roku 300 př. n. l.). Hlavní dílo: Euklidovy Základy (ve 13 kapitolách). Po Bibli nejvíce publikované dílo až do 19. století. Pokusil se o přesné formální vyjadřování, vybudoval geometrii systémem definice, věta, důkaz. Pokusil se definovat i nedefinovatelné: bod je to, co nemá části, křivka je délka bez šířky, přímka je křivka s body, která leží rovně, rozdělením přímého úhlu na dva stejné vzniká úhlel pravý,... Euklidovy postuláty (axiomy) BI-LIN, eprostor, 16, P. Olšák [3] Otazníky kolem pátého axiomu BI-LIN, eprostor, 16, P. Olšák [4] Euklides si uvědomil, že některá tvrzení nelze dokázat, je nutné je předpokládat. Formuloval pět tzv. postulátů: Dva body určují jedinou úsečku, která v těch bodech končí. Každá úsečka může být prodloužena tak, že vznikne opět úsečka. Je možné nakreslit kružnici s libovolným středem a poloměrem. Všechny pravé úhly jsou si rovny. Jestliže přímka protíná dvě přímky tak, že vnitřní úhly na téže straně jsou menší než dva pravé úhly, pak se tyto dvě přímky protnou na stejné straně, na které jsou úhly menší než dva pravé. Pátý axiom je formulován složitě, je v geometrii nutný? Ukázalo se, že pátý axiom je (za předpokladu platnosti prvních čtyř) ekvivalentní s následujícími tvrzeními: Daným bodem lze k dané přímce vést jedinou rovnoběžku. Trojúhelníky mají součet vnitřních úhlů 180. Platí Pythagorova věta. Později se ukázalo (Gauss, Lobačevskij, Riemann), že užitečná je i geometrie bez pátého axiomu (tzv. neeuklidovská geometrie). Například dvourozměrná geometrie na sféře: trojúhelníky mají součet úhlů větší než 180, každé dvě přímky (nejkratší spojnice dvou bodů prodloužené na obou koncích) se protínají, tj. neexistuje rovnoběžka. Neplatí Pythagorova věta.
2 Euklidovský prostor dnes BI-LIN, eprostor, 16, P. Olšák [5] BI-LIN, eprostor, 16, P. Olšák [6] Základní objekty v euklidovském prostoru V euklidovském prostoru chceme pracovat s přímkami (to umíme v afinním prostoru), dále chceme v rovinách vymezit kružnice. K tomu potřebujeme měřit vzdálenosti. Potřebujeme tedy metrický prostor. Metrika musí být odvozena z Pythagorovy věty (jinak by tato věta neplatila a neplatil by pátý Euklidův axiom). Tuto vlastnost splňuje metrika odvozená ze skalárního součinu. Konečně v euklidovském prostoru potřebujeme měřit úhly. K tomu také slouží skalární součin. Dnešní definice euklidovského prostoru je tedy následující: Definice: Euklidovský prostor E n je afinní prostor (X, V) dimenze n, přitom V je lineární prostor se skalárním součinem. Z tohoto součinu je odvozena norma a metrika na V. Metrika na X je definována takto: vzdálenost bodů P, Q je rovna velikosti vektoru P Q. Přímka: p = {A + t s, t R}, kde A X, s V, s o. Přímka je tedy dána bodem A, kterým prochází a nenulovým směrovým vektorem s. Může být též dána dvěma body A a B: p = {A + t (B A), t R}. Úsečka s koncovými body A, B: u = {A + t (B A), t 0, 1 }. Kružnice se středem S a poloměrem r: k = {X, ρ(s, X) = r}. Kružnici lze takto definovat jen v E 2 (dimenzi 2). Pro větší dimenze je uvedená množina povrchem n-rozměrné koule. Rovina: σ = {A + t a + u b, t, u R}, A X, a, b V jsou LN. Rovina je dána bodem a dvěma nezávislými směry. Zobecněná rovina (afinní podprostor): τ = A + a 1,..., a k, Vztahy mezi přímkami BI-LIN, eprostor, 16, P. Olšák [7] Příklad BI-LIN, eprostor, 16, P. Olšák [8] Dvě přímky p = {A 1 + t s 1, t R} a q = {A 2 + t s 2, t R} jsou totožné, právě když vektory A 2 A 1 a s 1 jsou LZ a současně směrové vektory s 1, s 2 jsou LZ. Dvě přímky p = {A 1 + t s 1, t R} a q = {A 2 + t s 2, t R} jsou rovnoběžné, právě když nejsou totožné a vektory s 1, s 2 jsou LZ. Dvě přímky p = {A 1 + t s 1, t R} a q = {A 2 + t s 2, t R} leží ve společné rovině, právě když vektory A 2 A 1, s 1, s 2 jsou LZ. Dvě přímky jsou různoběžky (protínají se v jednom bodě), právě když leží ve společné rovině a nejsou totožné ani rovnoběžné. Dvě přímky jsou mimoběžky (míjejí se v prostoru), právě když neleží ve společné rovině. Uvedené vztahy rozpoznáme algebraickými metodami: vyšetřením lineární závislosti nebo nezávislosti vektorů. Najdeme parametr a R takový, aby se přímky p = (1, 2, 3) + (2, 2, 5) a q = (4, 3, 7) + (3, a, 1) protínaly. Řešení: Přímky nejsou rovnoběžné ani totožné, protože jejich směrové vektory jsou lineárně nezávislé. Aby tyto přímky byly různoběžkami, musí být vektory (3, 1, 4), (2, 2, 5), (3, a, 1) lienárně závislé, takže když jejich souřadnice zapíšeme do řádků matice A, musí mít tato matice nulový determinant: det = 5 7a = 0. 3 a 1 Takže a = 5 7.
3 Zobecněná rovina: afinní podprostor BI-LIN, eprostor, 16, P. Olšák [9] Je dán bod A X a lineárně nezávislé vektory u 1, u 2,..., u k v afiním prostoru (X, V). Množině M = A + u 1, u 2,..., u k říkáme zobecněná rovina. Má dimenzi k. Zobecněná rovina dimenze 1 je přímka. Zobecněná rovina dimenze 2 je skutečná rovina. Pojem zobecněná rovina tedy zahrnuje pojmy přímka a rovina dokonce pro lineární prostory libovolné dimenze n. Zobecněná rovina je podprostor v afinním prostoru (X, V). Přesněji, při označení W = u 1, u 2,..., u k je dvojice (M, W) afinní podprostor: operace afinního prostoru jsou na množině M a lineárním podprostoru W uzavřeny. Vzájemná poloha zobecněných rovin BI-LIN, eprostor, 16, P. Olšák [10] Označme U = u 1, u 2,..., u k a V = v 1, v 2,..., v m. Necht A a B jsou body v afinním prostoru (X, V) a necht jsou dány dvě zobecněné roviny M = A + U a N = B + V. M a N jsou totožné, právě když U = V a A B U. M je obsažena v N, právě když U V a A B V. Další pojmy se týkají jen zobecněných rovin M a N takových, že žádná není obsažena v druhé. M je rovnoběžná s N, právě když U V nebo V U. Zobecněné roviny M a N se protínají, právě když A B U V. Zobecněné roviny jsou mimoběžné, právě když nejsou rovnoběžné a neprotínají se. M a N jsou na sebe kolmé, právě když u i v j = 0 pro všechna i {1,..., k} a j {1,..., m} Kartézský souřadný systém BI-LIN, eprostor, 16, P. Olšák [11] Idea analytické geometrie BI-LIN, eprostor, 16, P. Olšák [12] Necht E n = (X, V) je euklidovský prostor. Kartézský souřadný systém tohoto prostoru je souřadnicový systém (O, B) afinního prostoru (X, V) takový, že báze (B) je ortonormální. Necht (x 1, x 2,..., x n ) a (y 1, y 2,..., y n ) jsou souřadnice vektorů x a y vzhledem ke kartézkému souřadnému systému. Pak x y = x1 y 1 + x 2 y x n y n, x = x x x2 n. Necht (a 1, a 2,..., a n ) a (a 1, a 2,..., a n) jsou souřadnice bodů A a A vzhledem ke kartézkému souřadnému systému. Pak vzdálenost těchto bodů se počítá podle Pythagorovy věty : ρ(a, A ) = A A = (a 1 a 1 )2 + (a 2 a 2 )2 + + (a n a n) 2. Geometrické úlohy lze řešit algebraicky přechodem k souřadnicím vzhledem ke kartézskému souřadnému systému. Geometrické konstrukce pravítkem a kružítkem v rovině sestávají z těchto elementárních úkonů: najít průsečík dvou přímek (pokud existuje), najít průsečík přímky s kružnicí (pokud existuje), najít průsečík dvou kružnic (pokud existuje). Všechny tyto úkoly lze převést na výpočet souřadnic hledaných průsečíků vzhledem ke kartézskému souřadnicovému systému, pokud jsou dány souřadnice výchozích objektů (souřadnice bodu a směrového vektoru přímky, souřadnice středu a hodnota poloměru kružnice).
4 Příklad: průsečík přímek BI-LIN, eprostor, 16, P. Olšák [13] Příklad: průsečík přímky a kružnice BI-LIN, eprostor, 16, P. Olšák [14] V E 2 jsou dány přímky p = (1, 2) + (3, 4) a q = (2, 0) + (1, 3). Vektory a body jsou dány v kartézských souřadnicích. Najdeme průsečík přímek p, q. Protože směrové vektory (3, 4) a (1, 3) jsou lineárně nezávislé, přímky se protínají (v E 2 neexistují mimoběžky). Průsečík najdeme v místě, pro které nastává rovnost: (1, 2) + t (3, 4) = (2, 0) + u (1, 3) To vede na soustavu dvou lineárních rovnic s neznámými t, u. Ta má řešení t = 1, u = 2, takže průsečík je v bodě P = (1, 2) + 1 (3, 4) = (4, 6). V E 2 je dána přímka p = (1, 2) + (3, 4) a kružnice k se středem (1, 1) a poloměrem 3. Najdeme jejich průsečíky. Vzdálenost středu kružnice od bodu (1, 2) + t (3, 4) na přímce je f(t) = (1 + 3t 1) 2 + (2 + 4t 1) 2 = 25t 2 + 8t + 1 Průsečík nastává v místě, kde (f(t)) 2 = 3 2, neboli 25t 2 + 8t 8 = 0, t 1,2 = 8 ± 54, 25 takže jsme našli dva průsečíky: (1, 2) ( 54 1 (3, 4) = , ) 54, 25 (1, 2) + 8 ( 54 1 (3, 4) = , ) Příklad: průsečík dvou kružnic BI-LIN, eprostor, 16, P. Olšák [15] BI-LIN, eprostor, 16, P. Olšák [16] Nekopírovat vždy konstrukci výpočtem Jsou dány kružnice k 1 se středem (1, 1) a poloměrem 3 a kružnice k 2 se středem (3, 4) a poloměrem 2. Najdeme jejich průsečíky. Průsečík má souřadnice (x, y), které vyhovují dvěma rovnicím: (x 1) 2 + (y 1) 2 = 3 2 (x 3) 2 + (y 4) 2 = 2 2 Odečtením rovnic dostáváme lineární rovnici 2x + 3y = 14. Dosazením x = 7 3 2y do první rovnice dostávéme kvadratickou rovnici 13y 2 80y+112 = 0, která má řešení y 1 = 4, y 2 = Použitím vzorce x = y dostáváme x 1 = 1 a x 2 = 49 13, takže hledané průsečíky jsou ( 49 P 1 = (1, 4), P 2 = 13, 28 ). 13 Ne vždy se vyplatí postupovat stejně jako při řešení úloh pravítkem a kružítkem jen výpočtem souřadnic postupně vznikajících průsečíků. Například sestrojení kolmice na danou přímku p procházející daným bodem P uděláme kružítkem tak, že zapíchneme kružítko s dostatečně velkým poloměrem do P a najdeme průsečíky na p. Pak píchneme kružítko do těchto průsečíků se shodným poloměrem větším než polovina vzdálenosti průsečíků a najdeme průsečíky kružnic. Jejich spojnice je hledaná kolmice. Analyticky ale stačí kolmici vyjádřit jako P + s, přičemž s je vektor kolmý na směrový vektor přímky p. Kolmý vektor k vektoru v rovině s = (u, v) je vektor s = ( v, u), protože skalární součin těchto dvou vektorů je nulový.
5 BI-LIN, eprostor, 16, P. Olšák [17] Dva popisy zobecněné roviny v E n, n 3 Zobecněná rovina M může být zadána dvěma způsoby: Bodem a směrovými vektory: M = A + u 1, u 2,..., u k. Soustavou lineárních rovnic Bx = b takovou, že souřadnice všech bodů zobecněné roviny M tvoří množinu jejích řešení. Tuto soustavu nazýváme soustavou zobecněné roviny M. Tyto dva popisy umíme převádět jeden na druhý: Je-li dána soustava zobecněné roviny, pak její směrové vektory jsou bázové vektory přidružené homogenní soustavy Bx = o a bod A je partikulární řešení soutavy. Je-li dána zobecněná rovina směrovými vektory, pak zapíšeme jejich souřadnice do řádků matice A a vyřešíme Ax = o. Bázi řešení zapíšeme do řádků matice B a pravou stranu zjistíme dosazením souřadnic bodu A za neznámý vektor x. Příklady popisů přímky a roviny v E 3 BI-LIN, eprostor, 16, P. Olšák [18] Přímka: Je popsána bodem a směrovým vektorem A + s. Často se tento popis rozepisuje do souřadnic jako x = a 1 + t s 1, y = a 2 + t s 2, z = a 3 + t s 3, t R. Přímku můžeme také popsat soustavou dvou rovnic Bx = b. Není to typické, ale předvedeme si to. Bázi řešení soustavy s jednou rovnicí s 1 x+s 2 y+s 3 z = 0 označíme (u 1, u 2, u 3 ), (v 1, v 2, v 3 ). Hledaná soustava má pak matici obsahující tyto dva řádky a pravou stranu: b 1 = u 1 a 1 + u 2 a 2 + u 3 a 3, b 2 = v 1 a 1 + v 2 a 2 + v 3 a 3. Rovina: Je popsána dvěma směrovými vektory A + u, v. Vyřešením homogenní soustavy dvou rovnic se souřadnicemi těchto vektorů v řádcích matice dostáváme bázový vektor (n 1, n 2, n 3 ). Rovinu pak můžeme popsat rovnicí roviny n 1 x + n 2 y + n 3 z = d, kde d = n 1 a 1 + n 2 a 2 + n 3 a 3. Průsečíky zobecněných rovin BI-LIN, eprostor, 16, P. Olšák [19] Příklad: průsečík přímky s rovinou BI-LIN, eprostor, 16, P. Olšák [20] Dvě zobecněné roviny se mohou protínat. Průnik pak tvoří bod nebo zobecněnou rovinu. Jak tento průnik nalezneme? Sestavíme soustavu první zob. roviny Bx = b a druhé zob. roviny B x = b. Řešíme pak soustavu, která vznikne sloučením těchto dvou soustav. Soustava má rozšířenou matici ( ) B b B b a její řešení popisuje průnik daných zobecněných rovin. Příklad: Průnik dvou rovin ax + by + cz = d a a x + b y + c z = d najdeme jako řešení soustavy a x + b y + c z = d a x + b y + c z = d Je dána přímka p = (1, 2, 3) + (2, 2, 1) a rovina M = (2, 3, 4) + (3, 3, 1), (3, 4, 3) v E 3. Najdeme jejich průsečík. Podle předchozí stránky bychom mohli přímku p popsat dvěma rovnicemi a rovinu M třetí rovnicí a pak vyřešit soutavu těchto tří rovnic. Ovšem v tomto případě se většinou postupuje jinak: Rovnice roviny M má tvar 5x 6y + 3z = 4 a přímka p má parametrické vyjádření x = 1 + 2t, y = 2 + 2t, z = 3 + t. Dosadíme parametrické vyjádření přímky do rovnice roviny: 5 (1 + 2t) 6 (2 + 2t) + 3 (3 + t) = 4. Tato rovnice s jednou proměnnou má řešení t = 2. Průsečík je P = (1, 2, 3) + 2 (2, 2, 1) = (5, 6, 5).
6 Kolmice k zobecněné rovině v E n BI-LIN, eprostor, 16, P. Olšák [21] Kolmice ve 2D a 3D BI-LIN, eprostor, 16, P. Olšák [22] Je dána zobecněná rovina dimenze k: M = A + u 1, u 2,..., u k. Kolmice k M vedená z bodu B je zobecněná rovina N dimenze n k, kterou lze zapsat ve tvaru N = B + u 1, u 2,..., u k = B + v 1, v 2,..., v n k. přičemž vektory v 1, v 2,..., v n k získáme následovně: Zvolíme kartézský souřadný systém a souřadnice vektorů vzhledem k tomuto souřadnému systému ztotožníme s vektory samotnými. Vektory v 1, v 2,..., v n k pak tvoří bázi řešení homogenní soustavy Ax = o, kde matice A obsahuje v řádcích vektory u 1, u 2,..., u k. Příklady: V euklidovském prostoru E 3 je kolmice k rovině přímka a kolmice ke přímce je rovina. Kolmici v E n počítáme řešením homogenní soustavy, jak bylo zmíněno na předchozí stránce. To je univerzální postup. V případě E 2 a E 3 jsou ještě jiné postupy: V E 2 platí: (a, b) = ( b, a). V E 3 platí pro lin. nezávislé vektory: u, v = u v, kde symbolem je označem vektorový součin. O něm si povíme více později. BI-LIN, eprostor, 16, P. Olšák [23] Kolmý průmět bodu do zobecněné roviny Je dána zobecněná rovina M = A + u 1, u 2,..., u k a bod B (typicky mimo M). Najdeme bod B M takový, že B B je vektor kolmý na M. Bodu B říkáme kolmý průmět bodu B do zobecněné roviny M. Bod B lze najít takto: sestrojíme kolmici K = B+ u 1, u 2,..., u k. Průnik M K obsahuje jediný bod B. Jiný postup*: skalárním součinem lze počítat kolmý průmět vektoru na vektor. Označme symbolem p i kolmý průmět vektoru B A na vektor u i. Pak je B = A + p i ( u i / u i ). Pozorování: V bodě B má zobecněná rovina M nejmenší vzdálenost od bodu B. Důkaz: Je-li C M, pak BB C tvoří pravoúhlý trojúhelník a můžeme použít Pythagorovu větu. BI-LIN, eprostor, 16, P. Olšák [24] Kolmý průmět zob. roviny do zob. roviny Představme si, že například hledáme kolmý průmět přímky do roviny. Nebo děláme něco podobného ve více dimenzích... Kolmý průmět zob. roviny N = B+ v 1, v 2,..., v m do zob. roviny M = A + u 1, u 2,..., u k spočítáme v následujících krocích: Najdeme u 1, u 2,..., u k = w 1, w 2,..., w n k. Označme K = B + v 1, v 2,..., v m, w 1, w 2,..., w n k. Je to zobecněná rovina, která je nejmenší taková, že obsahuje zobecněnou rovinu N a současně obsahuje směr kolmý na M. Hledaný kolmý průmět je průnik M K.
7 Příklad: Kolmý průmět BI-LIN, eprostor, 16, P. Olšák [25] BI-LIN, eprostor, 16, P. Olšák [26] Determinant měří objem rovnoběžnostěnu Je dána přímka p = (1, 2, 3) + (5, 2, 2). Najdeme kolmý průmět této přímky do roviny M = (2, 2, 1) + (1, 3, 4), (3, 2, 6). Souřadnice jsou dány vzhledem ke kartézskému souřadnému systému. Řešením homogenní soustavy s maticí ( ) ( ) je (10, 6, 7), takže (1, 3, 4), (3, 2, 6) = (10, 6, 7). Kolmá rovina k M obsahující p je K = (1, 2, 3) + (5, 2, 2), (10, 6, 7). Rovnice roviny M je 10x + 6y 7z = 25 a rovnice K je 26x + 55y + 10z = 114. Hledaný průmět je řešení soustavy s maticí ( ) ( Hledaný průmět je p = ( 524/41, 0, 895/41) + (445, 41, 353). ). Necht v 1, v 2,..., v n jsou vektory, které tvoří hrany pomyslného n-dimenzionálního rovnoběžnostěnu. Vektory tvoří jen hrany, které se potkávají ve společném vrcholu. Ostatní hrany rovnoběžnostěnu je třeba dorýsovat doplněním na rovnoběžníky. Tvrzení: Zapíšeme-li do sloupců matice A souřadnice vektorů v i vzhledem k ortonormální bázi (B), pak absolutní hodnota determinantu matice A je rovna objemu zmíněného rovnoběžnostěnu. Idea důkazu*: Jsou-li vektory LZ, pak je zřejmě objem nulový a je det A = 0. Jsou-li v i LN, tvoří bázi a je možné ji Schmidtovým ortogonalizačním procesem upravit na ortonormální bázi (C). Napíšeme do sloupců matice R souřadnice v i vzhledem k (C). Pak det R je roven objemu rovnoběžnostěnu (důkaz indukcí, v indukčním kroku se použije vzorec základna krát výška ). Matice přechodu od (B) k (C) je ortogonální a je tedy det A = det(p B C R) = det P B C det R = ±1 det R Příklady BI-LIN, eprostor, 16, P. Olšák [27] Orientace lineárního prostoru BI-LIN, eprostor, 16, P. Olšák [28] Souřadnice uvedených bodů jsou v těchto příkladech vzhledem ke kartézskému souřadnému systému. Plocha rovnoběžníka s vrcholy (0, 0), (a, b) (c, d), (a + c, b + d) je rovna ( ) a b det = ad bc, c d Objem čtyřstenu s vrcholy (0, 0, 0), (a 1,a 2,a 3 ), (b 1,b 2,b 3 ), (c 1,c 2,c 3 ) je roven 1 a 1 b 1 c 1 6 det a 2 b 2 c 2 a 3 b 3 c, 3 protože čtyřstěn má objem roven jedné šestině objemu rovnoběžnostěnu. Souřadnice můžeme zapsat i do řádků, protože det A = det A T. V lineárním prostoru zvolíme jednu uspořádanou bázi (B) a prohlásíme ji kladně orientovanou. Všechny báze (C), pro které je det P B C > 0, nazveme také kladně orientované. Všechny báze (C ), pro které je det P B C < 0, nazveme záporně orientované. Obvyklá úmluva pro E 2 : kladně orientovaná báze má druhý bázový vektor směřující vlevo od prvního. Obvyklá úmluva pro E 3 : když se na bázi díváme z vhodného místa, pak kladně orientovaná báze má první vektor orientovaný k nám, druhý doprava od nás a třetí nahoru. Pozorovnání: determinant použitý při výpočtu objemu rovnoběžnostěnu je záporný, když souřadnice vektorů v 1, v 2,..., v n jsou zapsány vzhledem ke kladně orientované ortonormální bázi a vektory v 1, v 2,..., v n samotné tvoří záporně orientovanou bázi.
8 Speciální vlastnosti v E 3 BI-LIN, eprostor, 16, P. Olšák [29] Vektorový součin BI-LIN, eprostor, 16, P. Olšák [30] Je možné definovat vektorový součin. Kolmice k rovině je přímka, směrový vektor této kolmice je normálový vektor roviny. Normálový vektor je možné hledat pomocí vektorového součinu. Rovina je dána jedinou rovnicí se třemi neznámými, koeficienty této rovnice jsou souřadnice jejího normálového vektoru. Definice: Vektorový součin dvou vektorů u a v z E 3 značíme u v a je to: nulový vektor, pokud jsou u a v lineárně závislé, jinak: vektor kolmý na rovinu u, v s velikostí plochy rovnoběžníka mezi u a v. Báze ( u, v, u v ) je kladně orientovaná. Pozorování: Vektorový součin je definován jednoznačně. Platí u v = u v sin α, kde α je úhel mezi vektory u a v. Věta: Jsou-li (u 1, u 2, u 3 ) a (v 1, v 2, v 3 ) souřadnice vektorů u a v vzhledem ke kladně orientované ortonormální bázi, pak u v má vzhledem k této bázi souřadnice: ( ) u 2 u 3 v 2 v, u 1 u 3 3 v 1 v, u 1 u 2 3 v 1 v 2 Důkaz*: technický, viz skriptum. Příklad: normálový vektor roviny BI-LIN, eprostor, 16, P. Olšák [31] Je dána rovina (2, 2, 2) + (1, 2, 3), (3, 1, 1). Najedeme její normálový vektor. Souřadnice jsou uvedeny vzhledem ke kladně orientovanému kartézskému souřadnému systému. Normálový vektor je roven vektorovému součinu (1, 2, 3) (3, 1, 1), protože ten je (podle definice) kolmý na oba směrové vektory. Podle věty o souřadnicích vektorového součinu je ( ) 2 3 (1, 2, 3) (3, 1, 1) = 1 1, , = ( 1, 8, 5) Rovnice roviny tedy je x + 8y 5z = 4. Jiná možnost, jak najdeme normálový vektor: vyřešíme homogenní soustavu s maticí ( ) Příklad: rovina daná třemi body BI-LIN, eprostor, 16, P. Olšák [32] Jsou-li dány tři body A, B, C, které neleží ve společné přímce, pak jimi prochází jediná rovina A + (B A), (C A). Normálový vektor roviny je (B A) (C A). Třeba jsou dány body (1, 1, 2), (2, 3, 5), (4, 2, 3) v kartézských souřadnicích. Pak rovina je dána vzorcem: (1, 1, 2) + (1, 2, 3), (3, 1, 1) Protože (1, 2, 3) (3, 1, 1) = ( 1, 8, 5), má rovina tento normálový vektor. Má tedy rovnici x + 8y 5z = d, přitom d = = 3.
9 Příklad: vzdálenost bodu od přímky BI-LIN, eprostor, 16, P. Olšák [33] Můžeme najít kolmý průmět bodu B do přímky (označíme B ) a dále spočítáme velikost vektoru B B. Ovšem v E 3 máme vektorový součin a můžeme úlohu řešit ještě jinak (efektivněji): Vzdálenost bodu B od přímky A+ s je výška rovnoběžníka vymezeného vektory B A, s a ta je rovna ploše rovnoběžníka dělená velikostí základny. Vzdálenost bodu B od přímky tedy je (B A) s. s Příklad: vzdálenost bodu od roviny BI-LIN, eprostor, 16, P. Olšák [34] Můžeme najít kolmý průmět bodu B do roviny (označíme B ) a dále spočítáme velikost vektoru B B. Ovšem v E 3 máme vektorový součin a můžeme úlohu řešit ještě jinak (efektivněji): Vzdálenost bodu B od roviny A + u, v je rovna výšce rovnoběžnostěnu se stranami B A, u, v s podstavou u, v. Tato výška je rovna objemu tohoto rovnoběžnostěnu děleno plocha podstavy. Vzdálenost bodu B od roviny tedy je det A u, v kde matice A obsahuje v řádcích (nebo ve sloupcích) souřadnice vektorů A B, u, v vzhledem k nějaké ortonormální bázi. Příklad: vzdálenost mimoběžek BI-LIN, eprostor, 16, P. Olšák [35] Příklad: kolmice v E 3 BI-LIN, eprostor, 16, P. Olšák [36] Vzdálenost mimoběžek A + u a B + v je rovna výšce rovnoběžnostěnu vymezeného vektory B A, u, v se základnou u, v. Takže vzdálenost je rovna objemu tohoto rovnoběžnostěnu deleno plochou základny: det A u, v kde matice A obsahuje v řádcích (nebo ve sloupcích) souřadnice vektorů A B, u, v vzhledem k nějaké ortonormální bázi. Kolmice k přímce je rovina, která má normálový vektor rovný směrovému vektoru přímky. Kolmice k rovině je přímka, která má směrový vektor rovný normálovému vektoru roviny. Rovina daná rovnicí ax + by + cz = d má normálový vektor (a, b, c), takže přechod od roviny ke kolmé přímce nebo od přímky ke kolmé rovině je snadný.
10 Úhly mezi přímkami a rovinami BI-LIN, eprostor, 16, P. Olšák [37] Příklad: plocha trojúhelníka ABC BI-LIN, eprostor, 16, P. Olšák [38] Úhel φ mezi vektory u a v vypočítáme ze vzorce pro skalární součin u v u v cos φ = u v, tj. φ = arccos u v. Úhel mezi dvěma přímkami je úhlel mezi směrovými vektory. Pokud φ > 90, je hledaný úhel 180 φ (nebo ve vzorci v čitateli použít absolutní hodnotu). Úhel mezi rovinami je úhel mezi jejich normálovými vektory. Pokud φ > 90, je hledaný úhel 180 φ (nebo ve vzorci v čitateli použít absolutní hodnotu). Úhel mezi přímkou a rovinou je 90 mínus úhel mezi směrovým vektorem přímky a normálovým vektorem roviny (ve vzorci v čitateli je třeba použít absolutní hodnotu). Trojúhelník má plochu poloviční ploše rovnoběžníka. V E 2 spočítáme plochu rovnoběžníka jako objem rovnoběžnostěnu v E 2, tedy spočítáme absolutní hodnotu determinantu matice A, která obsahuje ve sloupcích souřadnice vektorů B A, C A vzhledem k ortonormální bázi. Příklad: A = (1, 2), B = (3, 4), C = (5, 8). Plocha trojúhelníka je: S = 1 ( ) det = V E 3 spočítáme plochu rovnoběžníka jeko velikost vektorového součinu vektorů B A, C A. Příklad: A = (1, 2, 2), B = (2, 3, 4), C = (7, 8, 9). S = 1 2 (1, 1, 2) (6, 6, 7) = 1 2 ( 5, 5, 0) = BI-LIN, eprostor, 16, P. Olšák [39] Úvaha*: k-dimensionální objem v E n. Jak spočítat např. plochu rovnoběžníka v E 4? Tam to není ani objem rovnoběžnostěnu, ani nemáme možnost použít vektorový součin. Odpověd najdeme v důkazu ze stránky [26]. Úloha: Jsou dány lineárně nezávislé vektory v 1, v 2,..., v k v E n, k n. Máme najít k-dimensionální objem v E n. Řešení: Vektory doplníme na bázi v 1, v 2,..., v k,..., v n a zapíšeme jejich souřadnice do sloupců matice A. Provedeme QR rozklad A = QR. Matici R zmenšíme na matici R k, která obsahuje jen prvních k řádků a k sloupců. Hledaný k dimenzionální objem je roven det R k. Poznámka: doplnění na bázi není prakticky potřeba dělat. Software dokáže provést i neúplný QR rozklad obdélníkové matice A = Q k R k. Zde matice A obsahuje ve sloupcích jen souřadnice vektorů v 1, v 2,..., v k.
Euklidovský prostor Stručnější verze
 [1] Euklidovský prostor Stručnější verze definice Eulidovského prostoru kartézský souřadnicový systém vektorový součin v E 3 vlastnosti přímek a rovin v E 3 a) eprostor-v2, 16, b) P. Olšák, FEL ČVUT, c)
[1] Euklidovský prostor Stručnější verze definice Eulidovského prostoru kartézský souřadnicový systém vektorový součin v E 3 vlastnosti přímek a rovin v E 3 a) eprostor-v2, 16, b) P. Olšák, FEL ČVUT, c)
Matematika 1 MA1. 1 Analytická geometrie v prostoru - základní pojmy. 4 Vzdálenosti. 12. přednáška ( ) Matematika 1 1 / 32
 Matematika 1 12. přednáška MA1 1 Analytická geometrie v prostoru - základní pojmy 2 Skalární, vektorový a smíšený součin, projekce vektoru 3 Přímky a roviny 4 Vzdálenosti 5 Příčky mimoběžek 6 Zkouška;
Matematika 1 12. přednáška MA1 1 Analytická geometrie v prostoru - základní pojmy 2 Skalární, vektorový a smíšený součin, projekce vektoru 3 Přímky a roviny 4 Vzdálenosti 5 Příčky mimoběžek 6 Zkouška;
1 Analytická geometrie
 1 Analytická geometrie 11 Přímky Necht A E 3 a v R 3 je nenulový Pak p = A + v = {X E 3 X = A + tv, t R}, je přímka procházející bodem A se směrovým vektorem v Rovnici X = A + tv, t R, říkáme bodová rovnice
1 Analytická geometrie 11 Přímky Necht A E 3 a v R 3 je nenulový Pak p = A + v = {X E 3 X = A + tv, t R}, je přímka procházející bodem A se směrovým vektorem v Rovnici X = A + tv, t R, říkáme bodová rovnice
Matematika I 12a Euklidovská geometrie
 Matematika I 12a Euklidovská geometrie Jan Slovák Masarykova univerzita Fakulta informatiky 3. 12. 2012 Obsah přednášky 1 Euklidovské prostory 2 Odchylky podprostorů 3 Standardní úlohy 4 Objemy Plán přednášky
Matematika I 12a Euklidovská geometrie Jan Slovák Masarykova univerzita Fakulta informatiky 3. 12. 2012 Obsah přednášky 1 Euklidovské prostory 2 Odchylky podprostorů 3 Standardní úlohy 4 Objemy Plán přednášky
Eukleidovský prostor a KSS Eukleidovský prostor je bodový prostor, ve kterém je definována vzdálenost dvou bodů (metrika)
 Eukleidovský prostor a KSS Eukleidovský prostor je bodový prostor, ve kterém je definována vzdálenost dvou bodů (metrika) Kartézská soustava souřadnic je dána počátkem O a uspořádanou trojicí bodů E x,
Eukleidovský prostor a KSS Eukleidovský prostor je bodový prostor, ve kterém je definována vzdálenost dvou bodů (metrika) Kartézská soustava souřadnic je dána počátkem O a uspořádanou trojicí bodů E x,
19 Eukleidovský bodový prostor
 19 Eukleidovský bodový prostor Eukleidovským bodovým prostorem rozumíme afinní bodový prostor, na jehož zaměření je definován skalární součin. Víme, že pomocí skalárního součinu jsou definovány pojmy norma
19 Eukleidovský bodový prostor Eukleidovským bodovým prostorem rozumíme afinní bodový prostor, na jehož zaměření je definován skalární součin. Víme, že pomocí skalárního součinu jsou definovány pojmy norma
6. ANALYTICKÁ GEOMETRIE
 Vektorová algebra 6. ANALYTICKÁ GEOMETRIE Pravoúhlé souřadnice bodu v prostoru Poloha bodu v prostoru je vzhledem ke třem osám k sobě kolmým určena třemi souřadnicemi, které tvoří uspořádanou trojici reálných
Vektorová algebra 6. ANALYTICKÁ GEOMETRIE Pravoúhlé souřadnice bodu v prostoru Poloha bodu v prostoru je vzhledem ke třem osám k sobě kolmým určena třemi souřadnicemi, které tvoří uspořádanou trojici reálných
Vzorce počítačové grafiky
 Vektorové operace součet vektorů rozdíl vektorů opačný vektor násobení vektoru skalárem úhel dvou vektorů velikost vektoru a vzdálenost dvojice bodů v rovině (v prostoru analogicky) u = B A= b a b a u
Vektorové operace součet vektorů rozdíl vektorů opačný vektor násobení vektoru skalárem úhel dvou vektorů velikost vektoru a vzdálenost dvojice bodů v rovině (v prostoru analogicky) u = B A= b a b a u
Euklidovské prostory. Euklidovský prostor dimense 3
 Euklidovské prostory Euklides nebo také Eukleides byl řecký matematik žijící kolem roku 300 př.n.l. Jeho nejznámějším dílem jsou Základy, ve kterých vybudoval geometrii způsobem definice- věta- důkaz.
Euklidovské prostory Euklides nebo také Eukleides byl řecký matematik žijící kolem roku 300 př.n.l. Jeho nejznámějším dílem jsou Základy, ve kterých vybudoval geometrii způsobem definice- věta- důkaz.
11 Vzdálenost podprostorů
 11 Vzdálenost podprostorů 11.1 Vzdálenost bodů Eukleidovský bodový prostor E n = afinní bodový prostor, na jehož zaměření je definován skalární součin. (Pech:AGLÚ/str.126) Definováním skalárního součinu
11 Vzdálenost podprostorů 11.1 Vzdálenost bodů Eukleidovský bodový prostor E n = afinní bodový prostor, na jehož zaměření je definován skalární součin. (Pech:AGLÚ/str.126) Definováním skalárního součinu
Necht L je lineární prostor nad R. Operaci : L L R nazýváme
 Skalární součin axiomatická definice odvození velikosti vektorů a úhlu mezi vektory geometrická interpretace ortogonalita vlastnosti ortonormálních bázi [1] Definice skalárního součinu Necht L je lineární
Skalární součin axiomatická definice odvození velikosti vektorů a úhlu mezi vektory geometrická interpretace ortogonalita vlastnosti ortonormálních bázi [1] Definice skalárního součinu Necht L je lineární
Projekt OPVK - CZ.1.07/1.1.00/ Matematika pro všechny. Univerzita Palackého v Olomouci
 Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Geometrie Různé metody řešení Téma: Analytická geometrie v prostoru, vektory, přímky Autor:
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Geometrie Různé metody řešení Téma: Analytická geometrie v prostoru, vektory, přímky Autor:
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ
 ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
x 2 = a 2 + tv 2 tedy (a 1, a 2 ) T + [(v 1, v 2 )] T A + V Příklad. U = R n neprázdná množina řešení soustavy Ax = b.
![x 2 = a 2 + tv 2 tedy (a 1, a 2 ) T + [(v 1, v 2 )] T A + V Příklad. U = R n neprázdná množina řešení soustavy Ax = b. x 2 = a 2 + tv 2 tedy (a 1, a 2 ) T + [(v 1, v 2 )] T A + V Příklad. U = R n neprázdná množina řešení soustavy Ax = b.](/thumbs/83/87395437.jpg) 1. Afinní podprostory 1.1. Motivace. Uvažujme R 3. Jeho všechny vektorové podprostory jsou počátek, přímky a roviny procházející počátkem a celé R 3. Chceme-li v R 3 dělat geometrii potřebujeme i jiné
1. Afinní podprostory 1.1. Motivace. Uvažujme R 3. Jeho všechny vektorové podprostory jsou počátek, přímky a roviny procházející počátkem a celé R 3. Chceme-li v R 3 dělat geometrii potřebujeme i jiné
Lineární algebra : Metrická geometrie
 Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních
Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních
Soustavy linea rnı ch rovnic
 [1] Soustavy lineárních rovnic vlastnosti množin řešení metody hledání řešení nejednoznačnost zápisu řešení a) soustavy, 10, b) P. Olšák, FEL ČVUT, c) P. Olšák 2010, d) BI-LIN, e) L, f) 2009/2010, g)l.
[1] Soustavy lineárních rovnic vlastnosti množin řešení metody hledání řešení nejednoznačnost zápisu řešení a) soustavy, 10, b) P. Olšák, FEL ČVUT, c) P. Olšák 2010, d) BI-LIN, e) L, f) 2009/2010, g)l.
Lingebraické kapitolky - Analytická geometrie
 Lingebraické kapitolky - Analytická geometrie Jaroslav Horáček KAM MFF UK 2013 Co je to vektor? Šipička na tabuli? Ehm? Množina orientovaných úseček majících stejný směr. Prvek vektorového prostoru. V
Lingebraické kapitolky - Analytická geometrie Jaroslav Horáček KAM MFF UK 2013 Co je to vektor? Šipička na tabuli? Ehm? Množina orientovaných úseček majících stejný směr. Prvek vektorového prostoru. V
14. přednáška. Přímka
 14 přednáška Přímka Začneme vyjádřením přímky v prostoru Přímku v prostoru můžeme vyjádřit jen parametricky protože obecná rovnice přímky v prostoru neexistuje Přímka v prostoru je určena bodem A= [ a1
14 přednáška Přímka Začneme vyjádřením přímky v prostoru Přímku v prostoru můžeme vyjádřit jen parametricky protože obecná rovnice přímky v prostoru neexistuje Přímka v prostoru je určena bodem A= [ a1
Rovnice přímky. s = AB = B A. X A = t s tj. X = A + t s, kde t R. t je parametr. x = a 1 + ts 1 y = a 2 + ts 2 z = a 3 + ts 3. t R
 Rovnice přímky Přímka p je určená dvěma různými body (A, B)(axiom) směrový vektor nenulový rovnoběžný (kolineární) s vektorem s = AB = B A pro libovolný bod X na přímce platí: X A = t s tj. Vektorová rovnice
Rovnice přímky Přímka p je určená dvěma různými body (A, B)(axiom) směrový vektor nenulový rovnoběžný (kolineární) s vektorem s = AB = B A pro libovolný bod X na přímce platí: X A = t s tj. Vektorová rovnice
transformace je posunutí plus lineární transformace má svou matici vzhledem k homogenním souřadnicím [1]
![transformace je posunutí plus lineární transformace má svou matici vzhledem k homogenním souřadnicím [1] transformace je posunutí plus lineární transformace má svou matici vzhledem k homogenním souřadnicím [1]](/thumbs/88/115112143.jpg) [1] Afinní transformace je posunutí plus lineární transformace má svou matici vzhledem k homogenním souřadnicím využití například v počítačové grafice Evropský sociální fond Praha & EU. Investujeme do
[1] Afinní transformace je posunutí plus lineární transformace má svou matici vzhledem k homogenním souřadnicím využití například v počítačové grafice Evropský sociální fond Praha & EU. Investujeme do
A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz
![A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz](/thumbs/47/23721460.jpg) 1/15 ANALYTICKÁ GEOMETRIE Základní pojmy: Soustava souřadnic v rovině a prostoru Vzdálenost bodů, střed úsečky Vektory, operace s vektory, velikost vektoru, skalární součin Rovnice přímky Geometrie v rovině
1/15 ANALYTICKÁ GEOMETRIE Základní pojmy: Soustava souřadnic v rovině a prostoru Vzdálenost bodů, střed úsečky Vektory, operace s vektory, velikost vektoru, skalární součin Rovnice přímky Geometrie v rovině
Soustavy. Terminologie. Dva pohledy na soustavu lin. rovnic. Definice: Necht A = (a i,j ) R m,n je matice, b R m,1 je jednosloupcová.
 [1] Terminologie [2] Soustavy lineárních rovnic vlastnosti množin řešení metody hledání řešení nejednoznačnost zápisu řešení Definice: Necht A = (a i,j ) R m,n je matice, b R m,1 je jednosloupcová matice.
[1] Terminologie [2] Soustavy lineárních rovnic vlastnosti množin řešení metody hledání řešení nejednoznačnost zápisu řešení Definice: Necht A = (a i,j ) R m,n je matice, b R m,1 je jednosloupcová matice.
M - Příprava na 1. čtvrtletku pro třídu 4ODK
 M - Příprava na 1. čtvrtletku pro třídu 4ODK Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu povoleno pouze s odkazem na www.jarjurek.cz. VARIACE 1 Tento dokument byl
M - Příprava na 1. čtvrtletku pro třídu 4ODK Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu povoleno pouze s odkazem na www.jarjurek.cz. VARIACE 1 Tento dokument byl
Analytická geometrie lineárních útvarů
 ) Na přímce: a) Souřadnice bodu na přímce: Analtická geometrie lineárních útvarů Bod P nazýváme počátek - jeho souřadnice je P [0] Nalevo od počátku leží čísla záporná, napravo čísla kladná. Každý bod
) Na přímce: a) Souřadnice bodu na přímce: Analtická geometrie lineárních útvarů Bod P nazýváme počátek - jeho souřadnice je P [0] Nalevo od počátku leží čísla záporná, napravo čísla kladná. Každý bod
1 Linearní prostory nad komplexními čísly
 1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
3. ÚVOD DO ANALYTICKÉ GEOMETRIE 3.1. ANALYTICKÁ GEOMETRIE PŘÍMKY
 3. ÚVOD DO ANALYTICKÉ GEOMETRIE 3.1. ANALYTICKÁ GEOMETRIE PŘÍMKY V této kapitole se dozvíte: jak popsat bod v rovině a v prostoru; vzorec na výpočet vzdálenosti dvou bodů; základní tvary rovnice přímky
3. ÚVOD DO ANALYTICKÉ GEOMETRIE 3.1. ANALYTICKÁ GEOMETRIE PŘÍMKY V této kapitole se dozvíte: jak popsat bod v rovině a v prostoru; vzorec na výpočet vzdálenosti dvou bodů; základní tvary rovnice přímky
Afinní transformace Stručnější verze
 [1] Afinní transformace Stručnější verze je posunutí plus lineární transformace má svou matici vzhledem k homogenním souřadnicím body a vektory: afinní prostor využití například v počítačové grafice a)
[1] Afinní transformace Stručnější verze je posunutí plus lineární transformace má svou matici vzhledem k homogenním souřadnicím body a vektory: afinní prostor využití například v počítačové grafice a)
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.
 INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 Báze vektorových prostorů, transformace souřadnic Michal Botur Přednáška
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 Báze vektorových prostorů, transformace souřadnic Michal Botur Přednáška
Vlastní číslo, vektor
 [1] Vlastní číslo, vektor motivace: směr přímky, kterou lin. transformace nezmění invariantní podprostory charakteristický polynom báze, vzhledem ke které je matice transformace nejjednodušší podobnost
[1] Vlastní číslo, vektor motivace: směr přímky, kterou lin. transformace nezmění invariantní podprostory charakteristický polynom báze, vzhledem ke které je matice transformace nejjednodušší podobnost
Vektorový prostor. Př.1. R 2 ; R 3 ; R n Dvě operace v R n : u + v = (u 1 + v 1,...u n + v n ), V (E 3 )...množina vektorů v E 3,
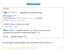 Vektorový prostor Příklady: Př.1. R 2 ; R 3 ; R n...aritmetický n-rozměrný prostor Dvě operace v R n : součet vektorů u = (u 1,...u n ) a v = (v 1,...v n ) je vektor u + v = (u 1 + v 1,...u n + v n ),
Vektorový prostor Příklady: Př.1. R 2 ; R 3 ; R n...aritmetický n-rozměrný prostor Dvě operace v R n : součet vektorů u = (u 1,...u n ) a v = (v 1,...v n ) je vektor u + v = (u 1 + v 1,...u n + v n ),
Těleso racionálních funkcí
 Těleso racionálních funkcí Poznámka. V minulém semestru jsme libovolnému oboru integrity sestrojili podílové těleso. Pro libovolné těleso R je okruh polynomů R[x] oborem integrity, máme tedy podílové těleso
Těleso racionálních funkcí Poznámka. V minulém semestru jsme libovolnému oboru integrity sestrojili podílové těleso. Pro libovolné těleso R je okruh polynomů R[x] oborem integrity, máme tedy podílové těleso
M - Příprava na 12. zápočtový test
 M - Příprava na 1. zápočtový test Určeno pro studenty dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu naleznete
M - Příprava na 1. zápočtový test Určeno pro studenty dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu naleznete
EUKLIDOVSKÉ PROSTORY
 EUKLIDOVSKÉ PROSTORY Necht L je lineární vektorový prostor nad tělesem reálných čísel R. Zobrazení (.,.) : L L R splňující vlastnosti 1. (x, x) 0 x L, (x, x) = 0 x = 0, 2. (x, y) = (y, x) x, y L, 3. (λx,
EUKLIDOVSKÉ PROSTORY Necht L je lineární vektorový prostor nad tělesem reálných čísel R. Zobrazení (.,.) : L L R splňující vlastnosti 1. (x, x) 0 x L, (x, x) = 0 x = 0, 2. (x, y) = (y, x) x, y L, 3. (λx,
9 Kolmost vektorových podprostorů
 9 Kolmost vektorových podprostorů Od kolmosti dvou vektorů nyní přejdeme ke kolmosti dvou vektorových podprostorů. Budeme se zabývat otázkou, kdy jsou dva vektorové podprostory na sebe kolmé a jak to poznáme.
9 Kolmost vektorových podprostorů Od kolmosti dvou vektorů nyní přejdeme ke kolmosti dvou vektorových podprostorů. Budeme se zabývat otázkou, kdy jsou dva vektorové podprostory na sebe kolmé a jak to poznáme.
maticeteorie 1. Matice A je typu 2 4, matice B je typu 4 3. Jakých rozměrů musí být matice X, aby se dala provést
 Úlohy k zamyšlení 1. Zdůvodněte, proč třetí řádek Hornerova schématu pro vyhodnocení polynomu p v bodě c obsahuje koeficienty polynomu r, pro který platí p(x) = (x c) r(x) + p(c). 2. Dokažte, že pokud
Úlohy k zamyšlení 1. Zdůvodněte, proč třetí řádek Hornerova schématu pro vyhodnocení polynomu p v bodě c obsahuje koeficienty polynomu r, pro který platí p(x) = (x c) r(x) + p(c). 2. Dokažte, že pokud
Matematika I, část I. Rovnici (1) nazýváme vektorovou rovnicí roviny ABC. Rovina ABC prochází bodem A a říkáme, že má zaměření u, v. X=A+r.u+s.
 3.4. Výklad Předpokládejme, že v prostoru E 3 jsou dány body A, B, C neležící na jedné přímce. Těmito body prochází jediná rovina, kterou označíme ABC. Určíme vektory u = B - A, v = C - A, které jsou zřejmě
3.4. Výklad Předpokládejme, že v prostoru E 3 jsou dány body A, B, C neležící na jedné přímce. Těmito body prochází jediná rovina, kterou označíme ABC. Určíme vektory u = B - A, v = C - A, které jsou zřejmě
Matematika I, část I Vzájemná poloha lineárních útvarů v E 3
 3.6. Vzájemná poloha lineárních útvarů v E 3 Výklad A. Vzájemná poloha dvou přímek Uvažujme v E 3 přímky p, q: p: X = A + ru q: X = B + sv a hledejme jejich společné body, tj. hledejme takové hodnoty parametrů
3.6. Vzájemná poloha lineárních útvarů v E 3 Výklad A. Vzájemná poloha dvou přímek Uvažujme v E 3 přímky p, q: p: X = A + ru q: X = B + sv a hledejme jejich společné body, tj. hledejme takové hodnoty parametrů
CVIČNÝ TEST 5. OBSAH I. Cvičný test 2. Mgr. Václav Zemek. II. Autorské řešení 6 III. Klíč 17 IV. Záznamový list 19
 CVIČNÝ TEST 5 Mgr. Václav Zemek OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 17 IV. Záznamový list 19 I. CVIČNÝ TEST 1 Zjednodušte výraz (2x 5) 2 (2x 5) (2x + 5) + 20x. 2 Určete nejmenší trojciferné
CVIČNÝ TEST 5 Mgr. Václav Zemek OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 17 IV. Záznamový list 19 I. CVIČNÝ TEST 1 Zjednodušte výraz (2x 5) 2 (2x 5) (2x + 5) + 20x. 2 Určete nejmenší trojciferné
CVIČNÝ TEST 13. OBSAH I. Cvičný test 2. Mgr. Zdeňka Strnadová. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 13 Mgr. Zdeňka Strnadová OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 V trojúhelníku ABC na obrázku dělí úsečka
CVIČNÝ TEST 13 Mgr. Zdeňka Strnadová OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 V trojúhelníku ABC na obrázku dělí úsečka
Matice. Je dána matice A R m,n, pak máme zobrazení A : R n R m.
 Matice lineárních zobrazení [1] Připomenutí Zobrazení A : L 1 L 2 je lineární, když A( x + y ) = A( x ) + A( y ), A(α x ) = α A( x ). Což je ekvivalentní s principem superpozice: A(α 1 x 1 + + α n x n
Matice lineárních zobrazení [1] Připomenutí Zobrazení A : L 1 L 2 je lineární, když A( x + y ) = A( x ) + A( y ), A(α x ) = α A( x ). Což je ekvivalentní s principem superpozice: A(α 1 x 1 + + α n x n
Vybrané kapitoly z matematiky
 Vybrané kapitoly z matematiky VŠB-TU Ostrava 2017-2018 Vybrané kapitoly z matematiky 2017-2018 1 / 19 Základní informace předmět: 714-0513, 5 kreditů přednáší: Radek Kučera kontakt: radek.kucera@vsb.cz,
Vybrané kapitoly z matematiky VŠB-TU Ostrava 2017-2018 Vybrané kapitoly z matematiky 2017-2018 1 / 19 Základní informace předmět: 714-0513, 5 kreditů přednáší: Radek Kučera kontakt: radek.kucera@vsb.cz,
X = A + tu. Obr x = a 1 + tu 1 y = a 2 + tu 2, t R, y = kx + q, k, q R (6.1)
 .6. Analtická geometrie lineárních a kvadratických útvarů v rovině. 6.1. V této kapitole budeme studovat geometrické úloh v rovině analtick, tj. lineární a kvadratické geometrické útvar vjádříme pomocí
.6. Analtická geometrie lineárních a kvadratických útvarů v rovině. 6.1. V této kapitole budeme studovat geometrické úloh v rovině analtick, tj. lineární a kvadratické geometrické útvar vjádříme pomocí
Matematika B101MA1, B101MA2
 Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Základní vlastnosti eukleidovského prostoru
 Kapitola 2 Základní vlastnosti eukleidovského prostoru 2.1 Eukleidovský prostor Eukleidovský prostor a jeho podprostory. Metrické vlastnosti, jako např. kolmost, odchylka, vzdálenost, obsah, objem apod.
Kapitola 2 Základní vlastnosti eukleidovského prostoru 2.1 Eukleidovský prostor Eukleidovský prostor a jeho podprostory. Metrické vlastnosti, jako např. kolmost, odchylka, vzdálenost, obsah, objem apod.
Lineární algebra : Skalární součin a ortogonalita
 Lineární algebra : Skalární součin a ortogonalita (15. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
Lineární algebra : Skalární součin a ortogonalita (15. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
PROSTORY SE SKALÁRNÍM SOUČINEM. Definice Nechť L je lineární vektorový prostor nad R. Zobrazení L L R splňující vlastnosti
 PROSTORY SE SKALÁRNÍM SOUČINEM Definice Nechť L je lineární vektorový prostor nad R. Zobrazení L L R splňující vlastnosti 1. (x, x) 0 x L, (x, x) = 0 x = 0, 2. (x, y) = (y, x) x, y L, 3. (λx, y) = λ(x,
PROSTORY SE SKALÁRNÍM SOUČINEM Definice Nechť L je lineární vektorový prostor nad R. Zobrazení L L R splňující vlastnosti 1. (x, x) 0 x L, (x, x) = 0 x = 0, 2. (x, y) = (y, x) x, y L, 3. (λx, y) = λ(x,
Lineární algebra : Skalární součin a ortogonalita
 Lineární algebra : Skalární součin a ortogonalita (15. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 30. dubna 2014, 09:00 1 2 15.1 Prehilhertovy prostory Definice 1. Buď V LP nad
Lineární algebra : Skalární součin a ortogonalita (15. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 30. dubna 2014, 09:00 1 2 15.1 Prehilhertovy prostory Definice 1. Buď V LP nad
Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y].
![Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y]. Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y].](/thumbs/91/104981778.jpg) Konzultace č. 6: Rovnice kružnice, poloha přímky a kružnice Literatura: Matematika pro gymnázia: Analytická geometrie, kap. 5.1 a 5. Sbírka úloh z matematiky pro SOŠ a studijní obory SOU. část, kap. 6.1
Konzultace č. 6: Rovnice kružnice, poloha přímky a kružnice Literatura: Matematika pro gymnázia: Analytická geometrie, kap. 5.1 a 5. Sbírka úloh z matematiky pro SOŠ a studijní obory SOU. část, kap. 6.1
Teorie informace a kódování (KMI/TIK) Reed-Mullerovy kódy
 Teorie informace a kódování (KMI/TIK) Reed-Mullerovy kódy Lukáš Havrlant Univerzita Palackého 10. ledna 2014 Primární zdroj Jiří Adámek: Foundations of Coding. Strany 137 160. Na webu ke stažení, heslo:
Teorie informace a kódování (KMI/TIK) Reed-Mullerovy kódy Lukáš Havrlant Univerzita Palackého 10. ledna 2014 Primární zdroj Jiří Adámek: Foundations of Coding. Strany 137 160. Na webu ke stažení, heslo:
Michal Zamboj. January 4, 2018
 Meziřádky mezi kuželosečkami - doplňkový materiál k přednášce Geometrie Michal Zamboj January 4, 018 Pozn. Najdete-li chybu, neváhejte mi napsat, může to ušetřit tápání Vašich kolegů. Pozn. v dokumentu
Meziřádky mezi kuželosečkami - doplňkový materiál k přednášce Geometrie Michal Zamboj January 4, 018 Pozn. Najdete-li chybu, neváhejte mi napsat, může to ušetřit tápání Vašich kolegů. Pozn. v dokumentu
ANALYTICKÁ GEOMETRIE V ROVINĚ
 ANALYTICKÁ GEOMETRIE V ROVINĚ Analytická geometrie vyšetřuje geometrické objekty (body, přímky, kuželosečky apod.) analytickými metodami. Podle prostoru, ve kterém pracujeme, můžeme analytickou geometrii
ANALYTICKÁ GEOMETRIE V ROVINĚ Analytická geometrie vyšetřuje geometrické objekty (body, přímky, kuželosečky apod.) analytickými metodami. Podle prostoru, ve kterém pracujeme, můžeme analytickou geometrii
[1] Motivace. p = {t u ; t R}, A(p) = {A(t u ); t R} = {t A( u ); t R}
![[1] Motivace. p = {t u ; t R}, A(p) = {A(t u ); t R} = {t A( u ); t R} [1] Motivace. p = {t u ; t R}, A(p) = {A(t u ); t R} = {t A( u ); t R}](/thumbs/26/7692117.jpg) Vlastní číslo, vektor motivace: směr přímky, kterou lin. transformace nezmění invariantní podprostory charakteristický polynom báze, vzhledem ke které je matice transformace nejjednodušší podobnost s diagonální
Vlastní číslo, vektor motivace: směr přímky, kterou lin. transformace nezmění invariantní podprostory charakteristický polynom báze, vzhledem ke které je matice transformace nejjednodušší podobnost s diagonální
6 Lineární geometrie. 6.1 Lineární variety
 6 Lineární geometrie Motivace. Pojem lineární varieta, který budeme v této kapitole studovat z nejrůznějších úhlů pohledu, není žádnou umělou konstrukcí. Příkladem lineární variety je totiž množina řešení
6 Lineární geometrie Motivace. Pojem lineární varieta, který budeme v této kapitole studovat z nejrůznějších úhlů pohledu, není žádnou umělou konstrukcí. Příkladem lineární variety je totiž množina řešení
Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice
 Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice Vektorové podprostory K množina reálných nebo komplexních čísel, U vektorový prostor nad K. Lineární kombinace vektorů u 1, u 2,...,u
Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice Vektorové podprostory K množina reálných nebo komplexních čísel, U vektorový prostor nad K. Lineární kombinace vektorů u 1, u 2,...,u
6. Vektorový počet Studijní text. 6. Vektorový počet
 6. Vektorový počet Budeme se pohybovat v prostoru R n, což je kartézská mocnina množiny reálných čísel R; R n = R R. Obvykle nám bude stačit omezení na případy n = 1, 2, 3; nicméně teorie je platná obecně.
6. Vektorový počet Budeme se pohybovat v prostoru R n, což je kartézská mocnina množiny reálných čísel R; R n = R R. Obvykle nám bude stačit omezení na případy n = 1, 2, 3; nicméně teorie je platná obecně.
(ne)závislost. α 1 x 1 + α 2 x 2 + + α n x n. x + ( 1) x Vektoru y = ( 1) y říkáme opačný vektor k vektoru y. x x = 1. x = x = 0.
 Lineární (ne)závislost [1] Odečítání vektorů, asociativita BI-LIN, zavislost, 3, P. Olšák [2] Místo, abychom psali zdlouhavě: x + ( 1) y, píšeme stručněji x y. Vektoru y = ( 1) y říkáme opačný vektor k
Lineární (ne)závislost [1] Odečítání vektorů, asociativita BI-LIN, zavislost, 3, P. Olšák [2] Místo, abychom psali zdlouhavě: x + ( 1) y, píšeme stručněji x y. Vektoru y = ( 1) y říkáme opačný vektor k
Skalární součin dovoluje zavedení metriky v afinním bodovém prostoru, tj. umožňuje nám určovat vzdálenosti, odchylky, obsahy a objemy.
 6 Skalární součin Skalární součin dovoluje zavedení metriky v afinním bodovém prostoru, tj. umožňuje nám určovat vzdálenosti, odchylky, obsahy a objemy. Příklad: Určete odchylku přímek p, q : p : x =1+3t,
6 Skalární součin Skalární součin dovoluje zavedení metriky v afinním bodovém prostoru, tj. umožňuje nám určovat vzdálenosti, odchylky, obsahy a objemy. Příklad: Určete odchylku přímek p, q : p : x =1+3t,
VEKTORY. Obrázek 1: Jediný vektor. Souřadnice vektoru jsou jeho průměty do souřadných os x a y u dvojrozměrného vektoru, AB = B A
 VEKTORY Vektorem se rozumí množina všech orientovaných úseček, které mají stejnou velikost, směr a orientaci, což vidíme na obr. 1. Jedna konkrétní orientovaná úsečka se nazývá umístění vektoru na obr.
VEKTORY Vektorem se rozumí množina všech orientovaných úseček, které mají stejnou velikost, směr a orientaci, což vidíme na obr. 1. Jedna konkrétní orientovaná úsečka se nazývá umístění vektoru na obr.
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
[1] Vzhledem ke zvolené bázi určujeme souřadnice vektorů...
![[1] Vzhledem ke zvolené bázi určujeme souřadnice vektorů... [1] Vzhledem ke zvolené bázi určujeme souřadnice vektorů...](/thumbs/13/23926.jpg) [1] Báze Každý lineární (pod)prostor má svou bázi Vzhledem ke zvolené bázi určujeme souřadnice vektorů... a) base, 4, b) P. Olšák, FEL ČVUT, c) P. Olšák 2010, d) BI-LIN, e) L, f) 2009/2010, g)l. Viz p.
[1] Báze Každý lineární (pod)prostor má svou bázi Vzhledem ke zvolené bázi určujeme souřadnice vektorů... a) base, 4, b) P. Olšák, FEL ČVUT, c) P. Olšák 2010, d) BI-LIN, e) L, f) 2009/2010, g)l. Viz p.
Učební texty k státní bakalářské zkoušce Matematika Skalární součin. študenti MFF 15. augusta 2008
 Učební texty k státní bakalářské zkoušce Matematika Skalární součin študenti MFF 15. augusta 2008 1 10 Skalární součin Požadavky Vlastnosti v reálném i komplexním případě Norma Cauchy-Schwarzova nerovnost
Učební texty k státní bakalářské zkoušce Matematika Skalární součin študenti MFF 15. augusta 2008 1 10 Skalární součin Požadavky Vlastnosti v reálném i komplexním případě Norma Cauchy-Schwarzova nerovnost
Shodná zobrazení. bodu B ležet na na zobrazené množině b. Proto otočíme kružnici b kolem
 Shodná zobrazení Otočení Příklad 1. Jsou dány tři různé soustředné kružnice a, b a c. Sestrojte rovnostranný trojúhelník ABC tak, aby A ležel na a, B ležel na b a C ležel na c. Řešení. Zvolíme vrchol A
Shodná zobrazení Otočení Příklad 1. Jsou dány tři různé soustředné kružnice a, b a c. Sestrojte rovnostranný trojúhelník ABC tak, aby A ležel na a, B ležel na b a C ležel na c. Řešení. Zvolíme vrchol A
Poznámka. V některých literaturách se pro označení vektoru také používá symbolu u.
 Vektory, operace s vektory Ž3 Orientovaná úsečka Mějme dvojici bodů, (na přímce, v rovině nebo prostoru), které spojíme a vznikne tak úsečka. Pokud budeme rozlišovat, zda je spojíme od k nebo od k, říkáme,
Vektory, operace s vektory Ž3 Orientovaná úsečka Mějme dvojici bodů, (na přímce, v rovině nebo prostoru), které spojíme a vznikne tak úsečka. Pokud budeme rozlišovat, zda je spojíme od k nebo od k, říkáme,
n tak, že součet vnitřních úhlů na jedné straně přímky k je méně než dva pravé úhly, pak se přímky m, straně protínají.
 Přednáška 5: Analytická geometrie v prostoru Geometrie stejně jako aritmetika stojí na několika málo základních principech. Díky tomu mohl již kolem roku 00 př. n. l. Eukleides napsat Základy 1, první
Přednáška 5: Analytická geometrie v prostoru Geometrie stejně jako aritmetika stojí na několika málo základních principech. Díky tomu mohl již kolem roku 00 př. n. l. Eukleides napsat Základy 1, první
IB112 Základy matematiky
 IB112 Základy matematiky Řešení soustavy lineárních rovnic, matice, vektory Jan Strejček IB112 Základy matematiky: Řešení soustavy lineárních rovnic, matice, vektory 2/53 Obsah Soustava lineárních rovnic
IB112 Základy matematiky Řešení soustavy lineárních rovnic, matice, vektory Jan Strejček IB112 Základy matematiky: Řešení soustavy lineárních rovnic, matice, vektory 2/53 Obsah Soustava lineárních rovnic
Matematika (CŽV Kadaň) aneb Úvod do lineární algebry Matice a soustavy rovnic
 Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Vektory a matice. Obsah. Aplikovaná matematika I. Carl Friedrich Gauss. Základní pojmy a operace
 Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
2. kapitola: Euklidovské prostory
 2. kapitola: Euklidovské prostory 2.1 Definice. Euklidovským n-rozměrným prostorem rozumíme neprázdnou množinu E n spolu s vektorovým prostorem V n a přiřazením, které každému bodu a z E n a každému vektoru
2. kapitola: Euklidovské prostory 2.1 Definice. Euklidovským n-rozměrným prostorem rozumíme neprázdnou množinu E n spolu s vektorovým prostorem V n a přiřazením, které každému bodu a z E n a každému vektoru
1 Báze a dimenze vektorového prostoru 1
 1 Báze a dimenze vektorového prostoru 1 Báze a dimenze vektorového prostoru 1 2 Aritmetické vektorové prostory 7 3 Eukleidovské vektorové prostory 9 Levá vnější operace Definice 5.1 Necht A B. Levou vnější
1 Báze a dimenze vektorového prostoru 1 Báze a dimenze vektorového prostoru 1 2 Aritmetické vektorové prostory 7 3 Eukleidovské vektorové prostory 9 Levá vnější operace Definice 5.1 Necht A B. Levou vnější
1. Parametrické vyjádření přímky Přímku v prostoru můžeme vyjádřit jen parametricky, protože obecná rovnice přímky v prostoru neexistuje.
 1/7 ANALYTICKÁ GEOMETRIE V PROSTORU Základní pojmy: Parametrické vyjádření přímky, roviny Obecná rovnice roviny Vzájemná poloha přímek a rovin Odchylka přímek a rovin Vzdálenosti www.karlin.mff.cuni.cz/katedry/kdm/diplomky/jan_koncel/
1/7 ANALYTICKÁ GEOMETRIE V PROSTORU Základní pojmy: Parametrické vyjádření přímky, roviny Obecná rovnice roviny Vzájemná poloha přímek a rovin Odchylka přímek a rovin Vzdálenosti www.karlin.mff.cuni.cz/katedry/kdm/diplomky/jan_koncel/
Operace s maticemi. 19. února 2018
 Operace s maticemi Přednáška druhá 19. února 2018 Obsah 1 Operace s maticemi 2 Hodnost matice (opakování) 3 Regulární matice 4 Inverzní matice 5 Determinant matice Matice Definice (Matice). Reálná matice
Operace s maticemi Přednáška druhá 19. února 2018 Obsah 1 Operace s maticemi 2 Hodnost matice (opakování) 3 Regulární matice 4 Inverzní matice 5 Determinant matice Matice Definice (Matice). Reálná matice
AB = 3 CB B A = 3 (B C) C = 1 (4B A) C = 4; k ]
![AB = 3 CB B A = 3 (B C) C = 1 (4B A) C = 4; k ] AB = 3 CB B A = 3 (B C) C = 1 (4B A) C = 4; k ]](/thumbs/93/113072660.jpg) 1. část 1. (u 1, u 2, u, u 4 ) je kladná báze orientovaného vektorového prostoru V 4. Rozhodněte, zda vektory (u, 2u 1 + u 4, u 4 u, u 2 ) tvoří kladnou, resp. zápornou bázi V 4. 0 2 0 0 0 0 0 1 0 2 0
1. část 1. (u 1, u 2, u, u 4 ) je kladná báze orientovaného vektorového prostoru V 4. Rozhodněte, zda vektory (u, 2u 1 + u 4, u 4 u, u 2 ) tvoří kladnou, resp. zápornou bázi V 4. 0 2 0 0 0 0 0 1 0 2 0
6.1 Vektorový prostor
 6 Vektorový prostor, vektory Lineární závislost vektorů 6.1 Vektorový prostor Nechť je dán soubor nějakých prvků, v němž je dána jistá struktura vztahů mezi jednotlivými prvky nebo v němž jsou předepsána
6 Vektorový prostor, vektory Lineární závislost vektorů 6.1 Vektorový prostor Nechť je dán soubor nějakých prvků, v němž je dána jistá struktura vztahů mezi jednotlivými prvky nebo v němž jsou předepsána
M - Pythagorova věta, Eukleidovy věty
 M - Pythagorova věta, Eukleidovy věty Určeno jako učební text pro studenty dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací
M - Pythagorova věta, Eukleidovy věty Určeno jako učební text pro studenty dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací
Úvod do lineární algebry
 Úvod do lineární algebry 1 Aritmetické vektory Definice 11 Mějme n N a utvořme kartézský součin R n R R R Každou uspořádanou n tici x 1 x 2 x, x n budeme nazývat n rozměrným aritmetickým vektorem Prvky
Úvod do lineární algebry 1 Aritmetické vektory Definice 11 Mějme n N a utvořme kartézský součin R n R R R Každou uspořádanou n tici x 1 x 2 x, x n budeme nazývat n rozměrným aritmetickým vektorem Prvky
1 Determinanty a inverzní matice
 Determinanty a inverzní matice Definice Necht A = (a ij ) je matice typu (n, n), n 2 Subdeterminantem A ij matice A příslušným pozici (i, j) nazýváme determinant matice, která vznikne z A vypuštěním i-tého
Determinanty a inverzní matice Definice Necht A = (a ij ) je matice typu (n, n), n 2 Subdeterminantem A ij matice A příslušným pozici (i, j) nazýváme determinant matice, která vznikne z A vypuštěním i-tého
příkladů do cvičení. V textu se objeví i pár detailů, které jsem nestihl (na které jsem zapomněl) a(b u) = (ab) u, u + ( u) = 0 = ( u) + u.
 Několik řešených příkladů do Matematiky Vektory V tomto textu je spočteno několik ukázkových příkladů které vám snad pomohou při řešení příkladů do cvičení. V textu se objeví i pár detailů které jsem nestihl
Několik řešených příkladů do Matematiky Vektory V tomto textu je spočteno několik ukázkových příkladů které vám snad pomohou při řešení příkladů do cvičení. V textu se objeví i pár detailů které jsem nestihl
1.1 Základní pojmy prostorové geometrie. Předmětem studia prostorové geometrie je prostor, jehož prvky jsou body. Další
 Kapitola 1 Planimetrie a stereometrie Doplňky ke středoškolské látce 1.1 Základní pojmy prostorové geometrie 1.1.1 Axiomy Předmětem studia prostorové geometrie je prostor, jehož prvky jsou body. Další
Kapitola 1 Planimetrie a stereometrie Doplňky ke středoškolské látce 1.1 Základní pojmy prostorové geometrie 1.1.1 Axiomy Předmětem studia prostorové geometrie je prostor, jehož prvky jsou body. Další
Dá se ukázat, že vzdálenost dvou bodů má tyto vlastnosti: 2.2 Vektor, souřadnice vektoru a algebraické operace s vektory
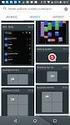 Vektorový počet.1 Eklidovský prostor E 3 Eklidovský prostor E 3 je prostor spořádaných trojic (tj. bodů), v němž je definována vzdálenost dvo jeho bodů A, B (značíme ji AB ). Vzdálenost bodů A = [a 1,
Vektorový počet.1 Eklidovský prostor E 3 Eklidovský prostor E 3 je prostor spořádaných trojic (tj. bodů), v němž je definována vzdálenost dvo jeho bodů A, B (značíme ji AB ). Vzdálenost bodů A = [a 1,
Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru. Kvadratická forma v n proměnných je tak polynom n proměnných s
 Kapitola 13 Kvadratické formy Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru f(x 1,..., x n ) = a ij x i x j, kde koeficienty a ij T. j=i Kvadratická forma v n proměnných
Kapitola 13 Kvadratické formy Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru f(x 1,..., x n ) = a ij x i x j, kde koeficienty a ij T. j=i Kvadratická forma v n proměnných
MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij]
![MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij]](/thumbs/58/41721403.jpg) MATICE Matice typu m/n nad tělesem T je soubor m n prvků z tělesa T uspořádaných do m řádků a n sloupců: a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] a m1 a m2 a mn Prvek a i,j je prvek matice A na místě
MATICE Matice typu m/n nad tělesem T je soubor m n prvků z tělesa T uspořádaných do m řádků a n sloupců: a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] a m1 a m2 a mn Prvek a i,j je prvek matice A na místě
6 Skalární součin. u v = (u 1 v 1 ) 2 +(u 2 v 2 ) 2 +(u 3 v 3 ) 2
 6 Skalární součin Skalární součin 1 je operace, která dvěma vektorům (je to tedy binární operace) přiřazuje skalár (v našem případě jde o reálné číslo, obecně se jedná o prvek nějakého tělesa T ). Dovoluje
6 Skalární součin Skalární součin 1 je operace, která dvěma vektorům (je to tedy binární operace) přiřazuje skalár (v našem případě jde o reálné číslo, obecně se jedná o prvek nějakého tělesa T ). Dovoluje
Úlohy k přednášce NMAG 101 a 120: Lineární algebra a geometrie 1 a 2,
 Úlohy k přednášce NMAG a : Lineární algebra a geometrie a Verze ze dne. května Toto je seznam přímočarých příkladů k přednášce. Úlohy z tohoto seznamu je nezbytně nutné umět řešit. Podobné typy úloh se
Úlohy k přednášce NMAG a : Lineární algebra a geometrie a Verze ze dne. května Toto je seznam přímočarých příkladů k přednášce. Úlohy z tohoto seznamu je nezbytně nutné umět řešit. Podobné typy úloh se
Afinita je stručný název pro afinní transformaci prostoru, tj.vzájemně jednoznačné afinní zobrazení bodového prostoru A n na sebe.
 4 Afinita Afinita je stručný název pro afinní transformaci prostoru, tj.vzájemně jednoznačné afinní zobrazení bodového prostoru A n na sebe. Poznámka. Vzájemně jednoznačným zobrazením rozumíme zobrazení,
4 Afinita Afinita je stručný název pro afinní transformaci prostoru, tj.vzájemně jednoznačné afinní zobrazení bodového prostoru A n na sebe. Poznámka. Vzájemně jednoznačným zobrazením rozumíme zobrazení,
1 Řešení soustav lineárních rovnic
 1 Řešení soustav lineárních rovnic 1.1 Lineární rovnice Lineární rovnicí o n neznámých x 1,x 2,..., x n s reálnými koeficienty rozumíme rovnici ve tvaru a 1 x 1 + a 2 x 2 +... + a n x n = b, (1) kde koeficienty
1 Řešení soustav lineárních rovnic 1.1 Lineární rovnice Lineární rovnicí o n neznámých x 1,x 2,..., x n s reálnými koeficienty rozumíme rovnici ve tvaru a 1 x 1 + a 2 x 2 +... + a n x n = b, (1) kde koeficienty
3 Lineární kombinace vektorů. Lineární závislost a nezávislost
 3 Lineární kombinace vektorů. Lineární závislost a nezávislost vektorů. Obrázek 5: Vektor w je lineární kombinací vektorů u a v. Vektory u, v a w jsou lineárně závislé. Obrázek 6: Vektor q je lineární
3 Lineární kombinace vektorů. Lineární závislost a nezávislost vektorů. Obrázek 5: Vektor w je lineární kombinací vektorů u a v. Vektory u, v a w jsou lineárně závislé. Obrázek 6: Vektor q je lineární
3.2. ANALYTICKÁ GEOMETRIE ROVINY
 3.2. ANALYTICKÁ GEOMETRIE ROVINY V této kapitole se dozvíte: jak popsat rovinu v třídimenzionálním prostoru; jak analyzovat vzájemnou polohu bodu a roviny včetně jejich vzdálenosti; jak analyzovat vzájemnou
3.2. ANALYTICKÁ GEOMETRIE ROVINY V této kapitole se dozvíte: jak popsat rovinu v třídimenzionálním prostoru; jak analyzovat vzájemnou polohu bodu a roviny včetně jejich vzdálenosti; jak analyzovat vzájemnou
1 Projekce a projektory
 Cvičení 3 - zadání a řešení úloh Základy numerické matematiky - NMNM20 Verze z 5. října 208 Projekce a projektory Opakování ortogonální projekce Definice (Ortogonální projekce). Uvažujme V vektorový prostor
Cvičení 3 - zadání a řešení úloh Základy numerické matematiky - NMNM20 Verze z 5. října 208 Projekce a projektory Opakování ortogonální projekce Definice (Ortogonální projekce). Uvažujme V vektorový prostor
11. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ
 11. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ Dovednosti: 1. Chápat pojmy orientovaná úsečka a vektor a geometrický význam součtu, rozdílu a reálného násobku orientovaných úseček a vektorů..
11. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ Dovednosti: 1. Chápat pojmy orientovaná úsečka a vektor a geometrický význam součtu, rozdílu a reálného násobku orientovaných úseček a vektorů..
Vzdálenosti. Copyright c 2006 Helena Říhová
 Vzdálenosti Copyright c 2006 Helena Říhová Obsah 1 Vzdálenosti 3 1.1 Vzdálenostivrovině... 3 1.1.1 Vzdálenostdvoubodů..... 3 1.1.2 Vzdálenostboduodpřímky..... 4 1.1.3 Vzdálenostdvourovnoběžek.... 5 1.2
Vzdálenosti Copyright c 2006 Helena Říhová Obsah 1 Vzdálenosti 3 1.1 Vzdálenostivrovině... 3 1.1.1 Vzdálenostdvoubodů..... 3 1.1.2 Vzdálenostboduodpřímky..... 4 1.1.3 Vzdálenostdvourovnoběžek.... 5 1.2
3) Vypočtěte souřadnice průsečíku dané přímky p : x = t, y = 9 + 3t, z = 1 + t, t R s rovinou ρ : 3x + 5y z 2 = 0.
 M1 Prog4 D1 1) Určete vektor c kolmý na vektory a = 2 i 3 j + k, b = i + 2 j 4 k. 2) Napište obecnou a parametrické rovnice roviny, která prochází bodem A[ 1; 1; 2] a je kolmá ke dvěma rovinám ρ : x 2y
M1 Prog4 D1 1) Určete vektor c kolmý na vektory a = 2 i 3 j + k, b = i + 2 j 4 k. 2) Napište obecnou a parametrické rovnice roviny, která prochází bodem A[ 1; 1; 2] a je kolmá ke dvěma rovinám ρ : x 2y
M - Příprava na 4. čtvrtletku - třídy 1P, 1VK.
 M - Příprava na 4. čtvrtletku - třídy 1P, 1VK. Učebnice určená pro přípravu na 4. čtvrtletní písemnou práci. Obsahuje učivo března až června. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a
M - Příprava na 4. čtvrtletku - třídy 1P, 1VK. Učebnice určená pro přípravu na 4. čtvrtletní písemnou práci. Obsahuje učivo března až června. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a
Přednáška 4: Soustavy lineárních rovnic
 Přednáška 4: Soustavy lineárních rovnic Touto přednáškou vrcholí naše snažení o algebraický popis řešení praktických problémů. Většina inženýrských úloh má totiž lineární charakter (alespoň přibližně)
Přednáška 4: Soustavy lineárních rovnic Touto přednáškou vrcholí naše snažení o algebraický popis řešení praktických problémů. Většina inženýrských úloh má totiž lineární charakter (alespoň přibližně)
VZÁJEMNÁ POLOHA DVOU PŘÍMEK
 VZÁJEMNÁ POLOHA DVOU PŘÍMEK VZÁJEMNÁ POLOHA DVOU PŘÍMEK p: a x b y c 0 q: a x b y c 0 ROVNOBĚŽNÉ PŘÍMKY (RŮZNÉ) nemají žádný společný bod, můžeme určit jejich vzdálenost, jejich odchylka je 0. Normálové
VZÁJEMNÁ POLOHA DVOU PŘÍMEK VZÁJEMNÁ POLOHA DVOU PŘÍMEK p: a x b y c 0 q: a x b y c 0 ROVNOBĚŽNÉ PŘÍMKY (RŮZNÉ) nemají žádný společný bod, můžeme určit jejich vzdálenost, jejich odchylka je 0. Normálové
2. ANALYTICKÁ GEOMETRIE V PROSTORU Vektory Úlohy k samostatnému řešení... 21
 2 ANALYTICKÁ GEOMETRIE V PROSTORU 21 21 Vektory 21 Úlohy k samostatnému řešení 21 22 Přímka a rovina v prostoru 22 Úlohy k samostatnému řešení 22 23 Vzájemná poloha přímek a rovin 25 Úlohy k samostatnému
2 ANALYTICKÁ GEOMETRIE V PROSTORU 21 21 Vektory 21 Úlohy k samostatnému řešení 21 22 Přímka a rovina v prostoru 22 Úlohy k samostatnému řešení 22 23 Vzájemná poloha přímek a rovin 25 Úlohy k samostatnému
FAKULTA STAVEBNÍ MATEMATIKA I MODUL GA01 M01 STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAM GEODÉZIE A KARTOGRAFIE S KOMBINOVANOU FORMOU STUDIA
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ MATEMATIKA I MODUL GA01 M01 VYBRANÉ ČÁSTI A APLIKACE VEKTOROVÉHO POČTU STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAM GEODÉZIE A KARTOGRAFIE S KOMBINOVANOU FORMOU STUDIA
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ MATEMATIKA I MODUL GA01 M01 VYBRANÉ ČÁSTI A APLIKACE VEKTOROVÉHO POČTU STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAM GEODÉZIE A KARTOGRAFIE S KOMBINOVANOU FORMOU STUDIA
a počtem sloupců druhé matice. Spočítejme součin A.B. Označme matici A.B = M, pro její prvky platí:
 Řešené příklady z lineární algebry - část 1 Typové příklady s řešením Příklady jsou určeny především k zopakování látky před zkouškou, jsou proto řešeny se znalostmi učiva celého semestru. Tento fakt se
Řešené příklady z lineární algebry - část 1 Typové příklady s řešením Příklady jsou určeny především k zopakování látky před zkouškou, jsou proto řešeny se znalostmi učiva celého semestru. Tento fakt se
FAKULTA STAVEBNÍ VUT V BRNĚ PŘIJÍMACÍ ŘÍZENÍ PRO AKADEMICKÝ ROK
 FAKULTA STAVEBNÍ VUT V BRNĚ PŘIJÍMACÍ ŘÍZENÍ PRO AKADEMICKÝ ROK 00 007 TEST Z MATEMATIKY PRO PŘIJÍMACÍ ZKOUŠKY ČÍSLO FAST-M-00-0. tg x + cot gx a) sinx cos x b) sin x + cos x c) d) sin x e) +. sin x cos
FAKULTA STAVEBNÍ VUT V BRNĚ PŘIJÍMACÍ ŘÍZENÍ PRO AKADEMICKÝ ROK 00 007 TEST Z MATEMATIKY PRO PŘIJÍMACÍ ZKOUŠKY ČÍSLO FAST-M-00-0. tg x + cot gx a) sinx cos x b) sin x + cos x c) d) sin x e) +. sin x cos
vyjádřete ve tvaru lineární kombinace čtverců (lineární kombinace druhých mocnin). Rozhodněte o definitnosti kvadratické formy κ(x).
 Řešené příklady z lineární algebry - část 6 Typové příklady s řešením Příklad 6.: Kvadratickou formu κ(x) = x x 6x 6x x + 8x x 8x x vyjádřete ve tvaru lineární kombinace čtverců (lineární kombinace druhých
Řešené příklady z lineární algebry - část 6 Typové příklady s řešením Příklad 6.: Kvadratickou formu κ(x) = x x 6x 6x x + 8x x 8x x vyjádřete ve tvaru lineární kombinace čtverců (lineární kombinace druhých
