Opakování ZŠ - Matematika - část geometrie - konstrukce
|
|
|
- Ján Čermák
- před 7 lety
- Počet zobrazení:
Transkript
1 Opakování ZŠ - Matematika - část geometrie - konstrukce Základní útvary v rovině Bod je nejzákladnější geometrický pojem. Body zapisujeme písmeny velké abecedy: A, B, N, H, Přímka Přímky zapisujeme písmeny malé abecedy: p, k, s, m, Polopřímka Bod ležící na přímce dělí přímku na dvě části, navzájem opačné polopřímky. Ty se zadávají také pomocí dvou bodů, záleží na jejich pořadí. První z nich je krajní bod, tzv. počátek. Polopřímku s počátkem A a vnitřním bodem B značíme AB. počátek polopřímky zápis: AB zápis: BA Úsečka Úsečku AB lze definovat jako průnik dvou polopřímek AB BA zápis: AB Velikost úsečky např.: AB 5cm Střed úsečky Body, které náleží úsečce a nejsou krajními, nazýváme vnitřní body úsečky. Ten z nich, který má od obou krajních bodů stejnou vzdálenost, je střed úsečky. Značíme S nebo s indexem např. S AB. 1
2 Nalezení středu úsečky pomocí kružítka a pravítka: Do kružítka vezmeme více než polovinu délky úsečka a okolo bodu A opíšeme kružnici (stačí část oblouk). Se stejným poloměrem opíšeme stejnou kružnici okolo bodu B. Obě kružnice se protnou ve dvou bodech, které označíme K, L a spojíme přímkou (osa úsečky). Průsečík této přímky a úsečky AB je hledaný střed S. 2
3 Úkol: Je dána úsečka AB, sestrojte její střed Úkol: Je dána trojice bodů A, B, C, vyznačte modře AB, červeně AC, zeleně CB. 3
4 Úhel Úhel je část roviny ohraničená dvěma polopřímkami, které mají společný počátek. Velikost úhlu - měří se: v stupňové míře - stupeň se dále dělí na minuty (značí se ) a vteřiny (značí se ). Jeden stupeň má 60 minut a jedna minuta má šedesát vteřin: 1 = 60', 1 = 60. v obloukové míře jednotkou je radián, jeho velikost odpovídá středovému úhlu oblouku, jehož délka je rovna poloměru daného oblouku. Významné úhly: stupně radiány Pravý úhel 90 π 2 Přímý úhel 180 π Plný úhel π Ostrý úhel jeho velikost je menší než 90 4
5 Tupý úhel jeho velikost je větší než 90 konvexní úhel (velikost méně než 180 ), nekonvexní úhel (velikost více než 180 ) Úkol: Ve stupňové míře změřte velikosti úhlů a zapište: Bylo nutné, všechny úhly měřit? Dají se využít některé vlastnosti? 5
6 Dvojice úhlů Vrcholové úhly jsou takové úhly, které mají společný vrchol a jejich ramena tvoří opačné polopřímky. Vrcholové úhly jsou vždy shodné, mají stejnou velikost. Vedlejší úhly jsou takové úhly, které mají jedno rameno společné a druhá ramena jsou opačné polopřímky. Součet vedlejších úhlů je vždy roven 180 (přímému úhlu). Rovnoběžky proťaté příčkou tvoří další dvojice shodných úhlů: Souhlasné úhly - na obrázku označeny. Střídavé úhly - na obrázku označeny. 6
7 Osa úhlu Je přímka, která prochází vrcholem úhlu a daný úhel půlí. Jak sestrojit osu úhlu pomocí kružítka a pravítka: Nejprve narýsujeme libovolně velkou kružnici (stačí pouze její část oblouk) se středem ve vrcholu úhlu, u kterého chceme osu udělat. Tato kružnice protne ramena úhlu vždy v jednom bodě, označme M a N. Poté vezmeme do kružítka opět libovolnou vzdálenost (nejlépe stejnou) a uděláme stejně velké kružnice postupně se středem v M a poté se středem v N. Tam, kde se kružnice protnou, se nachází jeden bod osy, bod označíme O. Druhý bod osy se nachází ve vrcholu úhlu. Spojíme O a V a získáme osu. 7
8 Jak přenést úhel kružítkem a pravítkem Začneme s tímto obrázkem: Úkolem je přenést úhel α výš tak, aby vrchol přeneseného úhlu α odpovídal bodu A, aby měl stejnou orientaci a aby spodní rameno leželo na přímce q. Narýsujeme část kružnice mezi rameny úhlu α o libovolném poloměru se středem ve vrcholu úhlu, A. V kružítku si ponechejme poloměr této kružnice. Nyní narýsujte stejnou část kružnice, o stejném poloměru, ale se středem v bodě A, tedy v místě, kde má být vrchol přenášeného úhlu. Tam, kde kružnice protne přímku q, se bude nacházet bod B. Nyní vezmeme do kružítka vzdálenost úsečky BD, zabodneme kružítko do bodu B a narýsujeme kružnici. V bodě, kde tato kružnice protne předchozí část kružnice, se nachází bod C. 8
9 Nyní už máme všechny tři body potřebné k sestrojení nového úhlu B A C. Sčítání a odečítání úhlů Pokud máme dva úhly, které potřebuje sečíst, můžeme použít tento postup. Vezmete jeden úhel, přenesete ho k druhému tak, aby měly jedno společné rameno, a výsledný úhel tvoří ramena, která mají ty dva úhly různá: V tomto příkladu je znázorněn součet α + β. Společné rameno polopřímka AC a různá ramena polopřímky AB a AD. Výsledek je úhel BAD. U odečítání to funguje velice podobně, akorát jeden úhel nepřenesete vně druhého úhlu, ale dovnitř úhlu. Poté od většího úhlu jakoby odečtete průnik těch dvou úhlů a máte rozdíl. Obrázek znázorňuje rozdíl α β. Červená část pak opět zvýrazňuje výsledný úhel. 9
10 Úkol: Je dán tupý úhel BAC, sestrojte jeho osu: Úkol: Sečtěte graficky úhly sestrojte úhel BAX o velikosti 10
11 Úkol: Doplňte velikosti všech úhlů Vzájemná poloha dvou přímek v rovině Na obrázku vidíme rovnoběžné přímky a, b, různoběžné přímky c, d, které se protínají v jednom bodě totožné přímky e, f. 11
12 Množina bodů dané vlastnosti Množinou M všech bodů dané vlastnosti V rozumíme takový geometrický útvar G, jehož všechny body splňují následující dvě podmínky: 1) Každý bod útvaru G má danou vlastnost V. 2) A obráceně, každý bod, který má danou vlastnost V, je bodem útvaru G. Osa o úsečky AB je množina všech bodů, které mají od bodů A a B stejnou vzdálenost. Množinou všech bodů, které mají od dané přímky p stejnou vzdálenost d cm, jsou dvě rovnoběžky q, r vzdálené o d cm od dané přímky p. 12
13 Množinou všech bodů, které mají od dvou různoběžných přímek stejnou vzdálenost, jsou osy úhlů vymezených těmito přímkami. Kružnice k (S;r) je množina všech bodů X roviny, které mají od bodu S vzdálenost r. 13
14 Čtyřúhelníky Základní prvky čtyřúhelníku: vrcholy: A, B, C, D strany: AB, BC, CD, AD dvojice protějších stran: AB a CD, BC a AD úhlopříčky: AC, BD vnitřní úhly: α, β, γ, δ součet vnitřních úhlů každého čtyřúhelníku je 360 Druhy čtyřúhelníků: Rovnoběžníky čtverec, obdélník, kosočtverec, kosodélník Lichoběžníky obecný, pravoúhlý, rovnoramenný Různoběžníky Čtverec Je to čtyřúhelník, který má velikosti všech stran shodné (a), každé dvě protější strany, jsou rovnoběžné, dvě sousední strany jsou navzájem kolmé. Vrcholy a strany čtverce ABCD označujeme písmeny abecedy v pořadí, jak jdou za sebou, a to v protisměru pohybu hodinových ručiček. Strana a leží vedle vrcholu A v protisměru hodinových ručiček, strana b vedle vrcholu B, strana c vedle vrcholu C a strana d vedle vrcholu D. Čtverec má čtyři stejně dlouhé strany a každý vnitřní úhel má velikost 90 stupňů. Každý čtverec ABCD má dvě úhlopříčky AC a DB. Úhlopříčka je vždy delší než strana čtverce. Pokud má strana čtverce velikost a, pak úhlopříčka u má velkost u = a 2 Úhlopříčky se navzájem půlí. Pokud vyznačíme střed čtverce bodem S (jako na obrázku), pak délka úsečky AS bude stejná jako délka úsečky CS. Úhlopříčka půlí úhel dvou sousedních stran. Například na obrázku má úhel ABC velikost 90 stupňů a úhel ABD má velikost 45 stupňů. Úhlopříčky spolu svírají pravý úhel. Obsah, odvod: o = 4a S = a 2 Obdélník Obdélník je čtyřúhelník, jehož všechny vnitřní úhly mají velikost 90 stupňů. Protilehlé strany obdélníku mají vždy stejnou velikost a jsou rovnoběžné. strany naproti sobě mají vždy stejnou délku, označujeme ji a a b Každý obdélník ABCD má dvě úhlopříčky AC a BD. 14
15 Úhlopříčky mají vždy stejnou velikost. Jsou zároveň vždy delší než kterákoliv strana obdélníku. Další vlastnosti úhlopříček: Délka úhlopříčky: u = a 2 + b 2, podle Pythagorovy věty. Úhlopříčky mezi sebou nesvírají pravý úhel. Úhlopříčky se navzájem půlí. Obsah, odvod: o =2a+2b = 2(a+b) S = a. b Úkol: Sestrojte obdélník ABCD, je-li dána strana a = 7 cm a úhlopříčka AC = 8,5 cm. Kosočtverec je rovnostranný rovnoběžník, který má všechny strany stejně dlouhé. Obecně jeho strany nesvírají pravý úhel. Dva protilehlé úhly mají stejnou velikost, dva sousední úhly dávají součet 180. Kosočtverec má dvě úhlopříčky. Jeho úhlopříčky jsou na sebe kolmé a půlí se a nemají shodné velikosti. Kosočtverec má dvě osy souměrnosti, kterými jsou úhlopříčky, a jeden střed souměrnosti, kterým je průsečík úhlopříček. Kosočtverci lze vepsat kružnici, která má střed v průsečíku úhlopříček. Obvod kosočtverce se vypočítá stejně jako u čtverce, protože má všechny strany stejně dlouhé Obsah, odvod: o = 4a S = a v a = b v b S = a b sinα 15
16 Úkol: Sestrojte kosočtverec ABCD, je-li AC =10 cm, BD =6 cm. Lichoběžník je čtyřúhelník, který má právě jednu dvojici rovnoběžných stran. Lichoběžníky se dělí na: obecný: ramena mají různé délky rovnoramenný: ramena mají stejné délky pravoúhlý: jedno rameno svírá se základnou pravý úhel a, c základna, b, d - ramena 16
17 Součet velikostí úhlů při jednom rameni je vždy 180. Součet velikostí všech vnitřních úhlů je 360 stupňů. Výška lichoběžníku je kolmá vzdálenost rovnoběžných stran. Úkol: Sestrojte lichoběžník ABCD (AB CD), je-li: a = 7 cm, c = 3 cm, = 75, v = 5 cm. Úkol: Sestrojte lichoběžník ABCD (AB CD), je-li: a = 8 cm, c = 4 cm, d = 5 dm, =
18 Úkol: Sestrojte lichoběžník ABCD (AB CD), je-li: a = 7 cm, c = 3 cm, IBDI = 6 dm, ABD = 45. Pravidelné n-úhelníky Konstrukce pravidelného šestiúhelníku o straně a = 5 cm: Sestrojíme kružnici k(s, r = 5 cm). Na kružnici libovolně zvolíme bod A a sestrojíme přímku AS. Přímka má s kružnicí společný bod D, A a D tvoří krajní body průměru. Sestrojíme kružnice k 1(A, r = 5 cm), k 2(D, r = 5cm). Tyto kružnice protnou kružnici k v bodech, jež jsou vrcholy pravidelného šestiúhelníku. 18
19 Úkol: Sestroj pravidelný šestiúhelník o straně a = 4 cm. Pravidelný osmiúhelník Konstrukce pravidelného osmiúhelníku, který je vepsán kružnici o poloměru r = 5 cm: Na kružnici k zvolíme libovolně bod A, sestrojíme přímku AS, a najdeme druhý krajní bod průměru bod E. Bodem S vedeme kolmici na přímku AS. Získáme dva body průměru CG. 19
20 Kružítkem sestrojíme osu úhlu CSA a bodem S vedeme na tuto osu kolmici. Získané průsečíky osy a kolmice s původní kružnicí jsou vrcholy osmiúhelníku. Úkol: Sestroj pravidelný osmiúhelník, který je vepsán kružnici o poloměru r = 4 cm. 20
21 Trojúhelník Trojúhelník ABC s vrcholy A, B, C lze definovat jako průnik tří polorovin ABC, BCA a CAB. Pokud tyto body leží v jedné přímce, potom takový trojúhelník neexistuje. Jedná se tedy o rovinný útvar ohraničený třemi úsečkami AB, AC, BC, které se nazývají strany trojúhelníku. Strany trojúhelníku splňují trojúhelníkové nerovnosti: Součet dvou libovolných stran je vždy delší než strana třetí: a + b > c a + c > b b + c > a, kde a, b, c jsou strany trojúhelníka. Součtem vnitřních úhlů trojúhelníku je úhel přímý (180 ). Úhly vedlejší k vnitřním úhlům, se nazývají vnější úhly trojúhelníka. Součet vnitřního a jeho vnějšího úhlu je 180. Součet dvou vnitřních úhlů se rovná vnějšímu úhlu u zbývajícího vrcholu. (např. 1 ) Druhy trojúhelníků: Podle stran Obecný trojúhelník (též různostranný) žádné dvě strany nejsou shodné Rovnoramenný trojúhelník dvě strany jsou navzájem shodné, ale nejsou shodné s třetí stranou Rovnostranný trojúhelník všechny strany jsou shodné Podle úhlů Ostroúhlý trojúhelník všechny vnitřní úhly jsou ostré Pravoúhlý trojúhelník jeden vnitřní úhel je pravý, zbývající dva jsou ostré Tupoúhlý trojúhelník jeden vnitřní úhel je tupý, zbývající dva jsou ostré Výšky trojúhelníku: Výška je kolmice spuštěná z vrcholu na protější stranu. Průsečík výšky s příslušnou stranou se nazývá pata výšky. 21
22 Každý trojúhelník má 3 výšky: Výšky: v a, v b, v c Střední příčky: Střední příčka je spojnice středů dvou stran. Střední příčka je rovnoběžná s příslušnou stranou a má velikost poloviny příslušné strany. Střední příčky dělí trojúhelník na 4 shodné trojúhelníky. Každý trojúhelník má 3 střední příčky: Střední příčky: : s a, s b, s c Středy stran: S a, S b, S c Těžnice trojúhelníku: Těžnice je spojnice vrcholu a středu protější strany. Těžnice se protínají v jednom bodě, který se nazývá těžiště T. Těžiště rozděluje každou těžnici na 2 díly v poměru 2:1 vzdálenost těžiště od vrcholu je dvojnásobek vzdálenosti od středu protější strany. Každá těžnice rozděluje trojúhelník na dva díly se stejným obsahem. Každý trojúhelník má 3 těžnice. Těžnice: t a, t b, t c Středy stran: S a, S b, S c Trojúhelníku lze opsat kružnici, kde střed kružnice opsané leží v průsečíku os stran a poloměr se rovná vzdálenosti středu od libovolného vrcholu. 22
23 Trojúhelníku lze vepsat kružnici, kde střed kružnice opsané leží v průsečíku os úhlů a poloměr se rovná vzdálenosti středu od libovolné strany. Úkol: Trojúhelníku ABC opište kružnici. Úkol: Trojúhelníku KLM vepište kružnici. 23
24 Příklad: Sestrojte trojúhelník ABC, ve kterém a = 5 cm, b= 7 cm, c = 8 cm. Součástí řešení úlohy je náčrtek s rozborem. Zápis konstrukce: 1) AB; AB = c = 8 cm 2) k; k(b; a = 5 cm) 3) l; l(a; b = 7 cm) 4) C; C k l 5) ABC Diskuse o počtu řešení: Úloha má ve zvolené polorovině jedno řešení. Úkol: Sestrojte trojúhelník ABC, ve kterém = 40, b = 4 cm, c = 5 cm. Úkol: Sestrojte trojúhelník ABC, ve kterém = 40, = 60, c = 8 cm. 24
25 Konstrukce trojúhelníku, je-li dána v zadání výška. Příklad: Sestrojte trojúhelník ABC, ve kterém c = 9 cm, v c= 5 cm, = 40. Jak sestrojíme bod C? Co o něm víme? Víme, že jeho kolmá vzdálenost od strany c je 5 cm (v c = 5 cm). Kde se tedy může nacházet bod splňující danou podmínku? Co je množinou všech bodů, jejichž kolmá vzdálenost od strany c je 5 cm? Je přímka rovnoběžná se stranou c, sestrojená ve vzdálenosti 5 cm. 1) AB; AB =c= 9 cm 2) q; q AB, q,ab =vc= 5 cm 3) BY; ABY = =40, 4) C; C q BY 5) ABC Ve zvolené polorovině má úloha jedno řešení. Pamatujte si! Je-li při konstrukci trojúhelníku zadána výška, použijeme ji většinou ve druhém kroku konstrukce k sestrojení rovnoběžky s příslušnou stranou ve vzdálenosti dané velikostí výšky. 25
26 Úkol: Sestrojte trojúhelník ABC, ve kterém c = 8 cm, v c = 4 cm, b = 5 cm. Úkol: Sestrojte trojúhelník ABC, jestliže b= 6 cm, a= 4,5 cm, v b= 3 cm. 26
27 Konstrukce trojúhelníku, známe-li jednu stranu a těžnici i výšku k ní příslušnou. Příklad: Sestrojte trojúhelník ABC, ve kterém c = 6 cm, v c = 4 cm, t c = 4,5 cm. Z předchozí úlohy víme, že začneme stranou c a druhým krokem bude sestrojení přímky p II AB ve vzdálenosti v c. Jak sestrojíme bod C pomocí zadané těžnice? Co o něm víme? Víme, že jeho vzdálenost od středu strany c je 4,5 cm (t c = 4,5 cm). Kde se tedy může nacházet bod splňující danou podmínku? Co je množinou všech bodů, jejichž vzdálenost od středu strany c je 4,5 cm? Je to kružnice se středem ve středu strany c a poloměrem o velikosti t c, tj. 4,5 cm. 1. AB; AB =c = 6 cm 2. p; p AB, p,ab =vc = 4 cm 3. Sc; Sc AB, ASc = ScB 4. k; k(sc; tc = 4,5 cm) 5. C 1, C 2; C 1, C 2 p k 6. ABC 1, ABC 2 Úloha má ve zvolené polorovině dvě řešení. Pamatujte si! Je-li při konstrukci trojúhelníku zadána těžnice, použijeme ji k sestrojení kružnice se středem ve středu příslušné strany a poloměrem o velikosti dané těžnice. 27
28 Úkol: Sestrojte trojúhelník ABC, jestliže c = 5 cm, v c = 3 cm, t c = 3 cm Konstrukce trojúhelníku, známe-li jednu stranu a dvě těžnice k ní nepříslušející. Příklad: Sestrojte trojúhelník ABC, ve kterém c = 9 cm, t a = 6 cm, t b = 9 cm. Ke konstrukci využijeme těžiště: těžiště dělí těžnice v poměru 2:1 tak, že delší úsek těžnice leží vždy u vrcholu. To znamená, že úsek těžnice od vrcholu do těžiště tvoří vždy 2/3 celkové délky těžnice. Začneme konstrukcí trojúhelníku ABT, prodloužíme polopřímky AT a BT, najdeme středy stran a a b a pomocí polopřímek AS b, BS a dokončíme konstrukci. 28
29 Zápis konstrukce 1) AB; AB =c= 9 cm 2) k; k(a; 2/3 t a= 4 cm) 3) l; l(b; 2/3 t b= 6 cm) 4) T; T k l 5) AT 6) m; m(t; 1/3 t a= 2 cm) 7) Sa; Sa AT m 8) BT 9) n; n(t; 1/3 t b= 3 cm) 10) S s; S s BT n 11) BS a 12) AS b 13) C; C BS a AS b 14) ABC Úloha má ve zvolené polorovině jedno řešení Konstrukce trojúhelníku, známe-li jednu stranu, jeden úhel k ní přilehlý a těžnici k dané straně Úkol: Sestrojte trojúhelník ABC, ve kterém c = 7 cm, = 60, t c = 4 cm. 29
30 Konstrukce trojúhelníku, známe-li jednu stranu, příslušnou výšku a poloměr kružnice opsané. Příklad: Sestrojte trojúhelník ABC, je-li dána délka strany a = 4,5 cm, v a = 2,5 cm a poloměr kružnice opsané r = 3,8 cm. Zápis konstrukce: 1. BCS (sss) 2. p; p II BC, p; BC = 2,5 cm 3. k; k(s; r = 3,8 cm) 4. A; A p k 5. ABC Ve zvolené polorovině má úloha dvě řešení. Úkol: Sestrojte trojúhelník ABC, je-li dána délka strany b = 5 cm, v b = 4 cm a poloměr kružnice opsané r = 3,5 cm. 30
31 Thaletova věta Jestliže ABC je pravoúhlý s přeponou AB, pak vrchol C (pravý úhel) leží na kružnici k s průměrem AB (platí pro libovolný ). (Tháles z Milétu asi př. n. l., řecký filosof, matematik a astronom) Thaletova kružnice - kružnice opsaná pravoúhlému Thaletova kružnice je taková kružnice, která má střed uprostřed přepony pravoúhlého trojúhelníku a poloměr rovný polovině přepony. Příklad: Sestrojte pravoúhlý trojúhelník ABC s pravým úhlem při vrcholu C, je-li c = 5 cm, v c = 2 cm. Náčrt a rozbor: 1) AB; AB = 5 cm 2) p; p AB ve vzdálenosti vc = 2 cm 3) S; S je střed AB 4) k; k (S; SA = 2,5 cm) 5) C; C p k 6) ABC Ve zvolené polorovině má úloha dvě řešení. 31
32 Úkol: Sestrojte pravoúhlý trojúhelník ABC s pravým úhlem při vrcholu C, je-li c = 6,6 cm, v c = 3 cm. Úkol: Sestrojte pravoúhlý trojúhelník ABC, ve kterém přepona c = 7 cm a odvěsna b = 5,5 cm. 32
33 Kružnice Množina všech bodů roviny, jejichž vzdálenost od bodu S je rovna r, se nazývá kružnice. Množina všech bodů roviny, jejichž vzdálenost od bodu S je menší než r nebo se rovná r, se nazývá kruh. S - střed kružnice r - poloměr kružnice AB = d - průměr kružnice; d = 2.r k (S, r) = kružnice k se středem v bodě S a poloměrem r S - střed kruhu, r - poloměr kruhu AB = d - průměr kruhu; d = 2.r M, N - body kruhu, N vnitřní bod K (S, r) = kruh K se středem v bodě S a poloměrem r Kružnice k(s, r) ohraničuje kruh K(S, r). Vzájemná poloha přímky a kružnice Vnější přímka - přímka, která nemá s kružnicí žádný společný bod Tečna - přímka, která má s kružnicí jeden společný bod Tečna je vždy v bodě dotyku kolmá na poloměr kružnice. 33
34 Sečna - přímka, která má s kružnicí dva společné body Sestrojení tečny ke kružnici: 1) Bod dotyku leží na kružnici Úkol: Sestrojte kružnici k(s; 2,5 cm). Na kružnici k zvolte bod T. Sestrojte tečnu, která je tečnou kružnice v bodě T. 2) Bod dotyku leží mimo kružnici Příklad: Je dána kružnice k(s; 3 cm). Na polopřímce SX zvolte bod M, tak aby ISMI = 5 cm. Z bodu M sestrojte tečnu ke kružnici, najděte bod dotyku T. 34
35 K řešení použijeme Thaletovu kružnici. Hledáme bod dotyku tečny, aby tečna splňovala podmínku, že je v bodě dotyku kolmá na poloměr, musí bod dotyku T ležet na Thaletově kružnici, body S a M tvoří krajní body průměru. Nejprve tedy najdeme střed úsečky SM bod P. Dále sestrojíme Thaletovu kružnici se středem P a poloměrem MP. Bod dotyku T je průsečíkem obou kružnic. Úloha má dvě řešení. Úkol: Je dána kružnice k a bod M. Z bodu M sestrojte tečnu ke kružnici, najděte bod dotyku T. 35
36 Vzájemná poloha dvou kružnic 1) soustředné kružnice = kružnice, které mají společný střed - nemají žádný společný bod. S 1=S 2 r 1 > r 2 k 1 k 2 = S 1S 2 = 0 cm 2) kružnice mají vnitřní dotyk. mají jeden společný bod T; T je bod dotyku kružnic se společnou tečnou t. S 1S 2 = r 1 - r 2 3) kružnice mají vnější dotyk. mají jeden společný bod T; T je bod dotyku kružnic se společnou tečnou t. r 1 + r 2 = S 1S 2 4) kružnice nemají žádný společný bod. r 1 - r 2 < r 1 + r 2 < S 1S 2 36
37 S 1S 2 < r 1 - r 2 Několik úloh závěrem: 1) Sestrojte trojúhelník, je-li dáno: a) a = 3 cm, b = 6 cm, = 30 b) c = 7,2cm, = 60, = 15 c) c = 8 cm, = 45, = 70 2) Sestrojte trojúhelník ABC, je-li dáno: a) a = 4,2 cm, va = 5 cm, = 30 b) c = 3,8 cm, b = 5,1 cm, tc = 5,1 cm c) * b = 3 cm, tc = 2,5 cm, ta = 4 cm (Návod: Využijte vlastnosti těžiště.) Geometrická zobrazení Osová souměrnost Definice: Je dána přímka o. Osová souměrnost s osou o je shodné zobrazení O(o), které přiřazuje: každému bodu X neležícímu na ose o bod X tak, že přímka o je osou úsečky XX, každému bodu Y ležícímu na ose o bod Y = Y. Osová souměrnost je jednoznačně určena osou souměrnosti. 37
38 Středová souměrnost Definice: je dán bod S. Středová souměrnost se středem S je shodné zobrazení S(S), které přiřazuje: 1. každému bodu X S bod X tak, že bod S je středem úsečky XX, 2. bodu S bod S = S středová souměrnost je jednoznačně určena středem S souměrnosti 38
Omezíme se jen na lomené čáry, jejichž nesousední strany nemají společný bod. Jestliže A 0 = A n (pro n 2), nazývá se lomená čára uzavřená.
 MNOHOÚHELNÍKY Vlastnosti mnohoúhelníků Lomená čára C 0 C C C 3 C 4 protíná samu sebe. Lomená čára A 0 A A... A n- A n (n ) se skládá z úseček A 0 A, A A,..., A n- A n, z nichž každé dvě sousední mají společný
MNOHOÚHELNÍKY Vlastnosti mnohoúhelníků Lomená čára C 0 C C C 3 C 4 protíná samu sebe. Lomená čára A 0 A A... A n- A n (n ) se skládá z úseček A 0 A, A A,..., A n- A n, z nichž každé dvě sousední mají společný
5. P L A N I M E T R I E
 5. P L A N I M E T R I E 5.1 Z Á K L A D N Í P L A N I M E T R I C K É P O J M Y Bod (definice, značení, znázornění) Přímka (definice, značení, znázornění) Polopřímka (definice, značení, znázornění, počáteční
5. P L A N I M E T R I E 5.1 Z Á K L A D N Í P L A N I M E T R I C K É P O J M Y Bod (definice, značení, znázornění) Přímka (definice, značení, znázornění) Polopřímka (definice, značení, znázornění, počáteční
Čtyřúhelník. O b s a h : Čtyřúhelník. 1. Jak definovat čtyřúhelník základní vlastnosti. 2. Názvy čtyřúhelníků Deltoid Tětivový čtyřúhelník
 Čtyřúhelník : 1. Jak definovat čtyřúhelník základní vlastnosti 2. Názvy čtyřúhelníků 2.1. Deltoid 2.2. Tětivový čtyřúhelník 2.3. Tečnový čtyřúhelník 2.4. Rovnoběžník 2.4.1. Základní vlastnosti 2.4.2. Výšky
Čtyřúhelník : 1. Jak definovat čtyřúhelník základní vlastnosti 2. Názvy čtyřúhelníků 2.1. Deltoid 2.2. Tětivový čtyřúhelník 2.3. Tečnový čtyřúhelník 2.4. Rovnoběžník 2.4.1. Základní vlastnosti 2.4.2. Výšky
Rozpis výstupů zima 2008 Geometrie
 Rozpis výstupů zima 2008 Geometrie 20. 10. porovnávání úseček grafický součet úseček grafický rozdíl úseček... porovnávání úhlů grafický součet úhlů grafický rozdíl úhlů... osa úhlu úhly vedlejší a vrcholové...
Rozpis výstupů zima 2008 Geometrie 20. 10. porovnávání úseček grafický součet úseček grafický rozdíl úseček... porovnávání úhlů grafický součet úhlů grafický rozdíl úhlů... osa úhlu úhly vedlejší a vrcholové...
PLANIMETRIE 2 mnohoúhelníky, kružnice a kruh
 PLANIMETRIE 2 mnohoúhelníky, kružnice a kruh Lomená čára A 0 A 1 A 2 A 3..., A n (n 2) se skládá z úseček A 0 A 1, A 1 A 2, A 2 A 3,..., A n 1 A n, z nichž každé dvě sousední mají společný jeden krajní
PLANIMETRIE 2 mnohoúhelníky, kružnice a kruh Lomená čára A 0 A 1 A 2 A 3..., A n (n 2) se skládá z úseček A 0 A 1, A 1 A 2, A 2 A 3,..., A n 1 A n, z nichž každé dvě sousední mají společný jeden krajní
Různostranný (obecný) žádné dvě strany nejsou stějně dlouhé. Rovnoramenný dvě strany (ramena) jsou stejně dlouhé, třetí strana je základna
 16. Trojúhelník, Mnohoúhelník, Kružnice (typy trojúhelníků a jejich vlastnosti, Pythagorova věta, Euklidovy věty, čtyřúhelníky druhy a jejich vlastnosti, kružnice obvodový a středový, úsekový úhel, vzájemná
16. Trojúhelník, Mnohoúhelník, Kružnice (typy trojúhelníků a jejich vlastnosti, Pythagorova věta, Euklidovy věty, čtyřúhelníky druhy a jejich vlastnosti, kružnice obvodový a středový, úsekový úhel, vzájemná
Úhly a jejich vlastnosti
 Úhly a jejich vlastnosti Pojem úhlu patří k nejzákladnějším pojmům geometrie. Zajímavé je, že úhel můžeme definovat několika různými způsoby, z nichž má každý své opodstatnění. Definice: Úhel je část roviny
Úhly a jejich vlastnosti Pojem úhlu patří k nejzákladnějším pojmům geometrie. Zajímavé je, že úhel můžeme definovat několika různými způsoby, z nichž má každý své opodstatnění. Definice: Úhel je část roviny
Trojúhelník a čtyřúhelník výpočet jejich obsahu, konstrukční úlohy
 5 Trojúhelník a čtyřúhelník výpočet jejich obsahu, konstrukční úlohy Trojúhelník: Trojúhelník je definován jako průnik tří polorovin. Pojmy: ABC - vrcholy trojúhelníku abc - strany trojúhelníku ( a+b>c,
5 Trojúhelník a čtyřúhelník výpočet jejich obsahu, konstrukční úlohy Trojúhelník: Trojúhelník je definován jako průnik tří polorovin. Pojmy: ABC - vrcholy trojúhelníku abc - strany trojúhelníku ( a+b>c,
PLANIMETRIE úvodní pojmy
 PLANIMETRIE úvodní pojmy Je část geometrie zabývající se studiem geometrických útvarů v rovině. Základními stavebními kameny v rovině budou bod a přímka. 1) Přímka a její části Dvěma různými body lze vést
PLANIMETRIE úvodní pojmy Je část geometrie zabývající se studiem geometrických útvarů v rovině. Základními stavebními kameny v rovině budou bod a přímka. 1) Přímka a její části Dvěma různými body lze vést
n =5, potom hledejte obecný vztah. 4.5 Mnohoúhelníky PŘÍKLAD 4.2. Kolik úhlopříček má n úhelník? Vyřešte nejprve pro Obrázek 28: Tangram
 4.5 Mnohoúhelníky Obrázek 28: Tangram Mnohoúhelník můžeme charakterizovat jako část roviny ohraničenou uzavřenou lomenou čarou (tj. čarou, která se skládá z na sebe navazujících úseček). Již víme, že rozlišujeme
4.5 Mnohoúhelníky Obrázek 28: Tangram Mnohoúhelník můžeme charakterizovat jako část roviny ohraničenou uzavřenou lomenou čarou (tj. čarou, která se skládá z na sebe navazujících úseček). Již víme, že rozlišujeme
2. Vyšetřete všechny možné případy vzájemné polohy tří různých přímek ležících v jedné rovině.
 ZS1BK_PGE1 Geometrie I: Vybrané úlohy z elementární geometrie 1. Které geometrické útvary mohou vzniknout a) jako průnik dvou polopřímek téže přímky, b) jako průnik dvou polorovin téže roviny? V případě
ZS1BK_PGE1 Geometrie I: Vybrané úlohy z elementární geometrie 1. Které geometrické útvary mohou vzniknout a) jako průnik dvou polopřímek téže přímky, b) jako průnik dvou polorovin téže roviny? V případě
Shodná zobrazení. bodu B ležet na na zobrazené množině b. Proto otočíme kružnici b kolem
 Shodná zobrazení Otočení Příklad 1. Jsou dány tři různé soustředné kružnice a, b a c. Sestrojte rovnostranný trojúhelník ABC tak, aby A ležel na a, B ležel na b a C ležel na c. Řešení. Zvolíme vrchol A
Shodná zobrazení Otočení Příklad 1. Jsou dány tři různé soustředné kružnice a, b a c. Sestrojte rovnostranný trojúhelník ABC tak, aby A ležel na a, B ležel na b a C ležel na c. Řešení. Zvolíme vrchol A
P L A N I M E T R I E
 M T E M T I K P L N I M E T R I E rovinná geometrie Základní planimetrické pojmy od - značí se velkými tiskacími písmeny, např.,,. P, Q. Přímka - značí se malými písmeny, např. a, b, p, q nebo pomocí bodů
M T E M T I K P L N I M E T R I E rovinná geometrie Základní planimetrické pojmy od - značí se velkými tiskacími písmeny, např.,,. P, Q. Přímka - značí se malými písmeny, např. a, b, p, q nebo pomocí bodů
Kružnice, úhly příslušné k oblouku kružnice
 KRUŽNICE, KRUH Kružnice, úhly příslušné k oblouku kružnice Je dán bod S a kladné číslo r. Kružnice k(s;r) je množina všech bodů (roviny), které mají od bodu S vzdálenost r. Můžeme také říci. Kružnicí k
KRUŽNICE, KRUH Kružnice, úhly příslušné k oblouku kružnice Je dán bod S a kladné číslo r. Kružnice k(s;r) je množina všech bodů (roviny), které mají od bodu S vzdálenost r. Můžeme také říci. Kružnicí k
Úsečka spojující sousední vrcholy se nazývá strana, spojnice nesousedních vrcholů je úhlopříčka mnohoúhelníku.
 Mnohoúhelníky Je dáno n různých bodů A 1, A 2,. A n, z nichž žádné tři neleží na přímce. Geometrický útvar tvořený lomenou čarou a částí roviny touto čarou ohraničenou nazýváme n-úhelníkem A 1 A 2. A n.
Mnohoúhelníky Je dáno n různých bodů A 1, A 2,. A n, z nichž žádné tři neleží na přímce. Geometrický útvar tvořený lomenou čarou a částí roviny touto čarou ohraničenou nazýváme n-úhelníkem A 1 A 2. A n.
DIDAKTIKA MATEMATIKY
 DIDAKTIKA MATEMATIKY GEOMETRIE PLANIMETRIE Úlohy k rozvoji geometrické představivosti Úlohy početní a důkazové Růžena Blažková, Irena Budínová Brno 2007 1 1. Základní pojmy 1. Zvolte si čtyři různé body
DIDAKTIKA MATEMATIKY GEOMETRIE PLANIMETRIE Úlohy k rozvoji geometrické představivosti Úlohy početní a důkazové Růžena Blažková, Irena Budínová Brno 2007 1 1. Základní pojmy 1. Zvolte si čtyři různé body
Konstrukční úlohy. Růžena Blažková, Irena Budínová. Milé studentky, milí studenti,
 Konstrukční úlohy Růžena Blažková, Irena Budínová Milé studentky, milí studenti, zadání konstrukčních úloh si vylosujete v semináři nebo na přednášce, u každé konstrukční úlohy proveďte: - rozbor obsahuje
Konstrukční úlohy Růžena Blažková, Irena Budínová Milé studentky, milí studenti, zadání konstrukčních úloh si vylosujete v semináři nebo na přednášce, u každé konstrukční úlohy proveďte: - rozbor obsahuje
GEOMETRIE PLANIMETRIE Úlohy k rozvoji geometrické představivosti Úlohy početní. Růžena Blažková
 GEOMETRIE PLANIMETRIE Úlohy k rozvoji geometrické představivosti Úlohy početní Růžena Blažková 1. Základní pojmy 1. Zvolte si čtyři různé body v rovině. Kolik různých přímek je těmito body určeno? Jak
GEOMETRIE PLANIMETRIE Úlohy k rozvoji geometrické představivosti Úlohy početní Růžena Blažková 1. Základní pojmy 1. Zvolte si čtyři různé body v rovině. Kolik různých přímek je těmito body určeno? Jak
[obr. 1] Rozbor S 3 S 2 S 1. o 1. o 2 [obr. 2]
![[obr. 1] Rozbor S 3 S 2 S 1. o 1. o 2 [obr. 2] [obr. 1] Rozbor S 3 S 2 S 1. o 1. o 2 [obr. 2]](/thumbs/51/27343209.jpg) Příklad Do dané kruhové výseče s ostrým středovým úhlem vepište kružnici (obr. ). M k l V N [obr. ] Rozbor Oblouk l a hledaná kružnice k se dotýkají v bodě T, mají proto v tomto bodě společnou tečnu t.
Příklad Do dané kruhové výseče s ostrým středovým úhlem vepište kružnici (obr. ). M k l V N [obr. ] Rozbor Oblouk l a hledaná kružnice k se dotýkají v bodě T, mají proto v tomto bodě společnou tečnu t.
TROJÚHELNÍK 180. Definice. C neleží v přímce. Potom trojúhelníkem ABC nazveme průnik polorovin ABC, BCA, Nechť body. Viz příloha: obecny_trojuhelnik
 TROJÚHELNÍK Definice Nechť body A, B, C neleží v přímce. Potom trojúhelníkem ABC nazveme průnik polorovin ABC, BCA, CAB. Viz příloha: obecny_trojuhelnik Definice trojúhelníku Uzavřená, jednoduchá (neprotínající
TROJÚHELNÍK Definice Nechť body A, B, C neleží v přímce. Potom trojúhelníkem ABC nazveme průnik polorovin ABC, BCA, CAB. Viz příloha: obecny_trojuhelnik Definice trojúhelníku Uzavřená, jednoduchá (neprotínající
6 Planimetrie. 6.1 Trojúhelník. body A, B, C vrcholy trojúhelníku. vnitřní úhly BAC = α, ABC = β, BCA = γ. konvexní (menší než 180º)
 6 Planimetrie Planimetrie = část matematiky, která se zabývá geometrií (původně věda o měřené země) v rovině (obrazce, jejich vlastnosti, shodnost a podobnost, zobrazení). 6.1 Trojúhelník Každé tři body,
6 Planimetrie Planimetrie = část matematiky, která se zabývá geometrií (původně věda o měřené země) v rovině (obrazce, jejich vlastnosti, shodnost a podobnost, zobrazení). 6.1 Trojúhelník Každé tři body,
Přípravný kurz - Matematika
 Přípravný kurz - Matematika Téma: Konstrukční úlohy Klíčová slova: rozbor, náčrt, popis, diskuse počtu řešení, kružnice opsaná a vepsaná Autor: trojúhelníku Mlynářová 12 19 9:02 Kontrukční úlohy Výsledkem
Přípravný kurz - Matematika Téma: Konstrukční úlohy Klíčová slova: rozbor, náčrt, popis, diskuse počtu řešení, kružnice opsaná a vepsaná Autor: trojúhelníku Mlynářová 12 19 9:02 Kontrukční úlohy Výsledkem
1. Planimetrie - geometrické útvary v rovině
 1. Planimetrie - geometrické útvary v rovině 1. Základní pojmy Body průsečíky čar, značí se velkými tiskacími písmeny A = B bod A je totožný (splývá) s bodem B A B různé body A, B Přímka je dána dvěma
1. Planimetrie - geometrické útvary v rovině 1. Základní pojmy Body průsečíky čar, značí se velkými tiskacími písmeny A = B bod A je totožný (splývá) s bodem B A B různé body A, B Přímka je dána dvěma
PRACOVNÍ SEŠIT PLANIMETRIE. 6. tematický okruh: Připrav se na státní maturitní zkoušku z MATEMATIKY důkladně, z pohodlí domova a online.
 Připrav se na státní maturitní zkoušku z MATEMATIKY důkladně, z pohodlí domova a online PRACOVNÍ SEŠIT 6. tematický okruh: PLANIMETRIE vytvořila: RNDr. Věra Effenberger expertka na online přípravu na SMZ
Připrav se na státní maturitní zkoušku z MATEMATIKY důkladně, z pohodlí domova a online PRACOVNÍ SEŠIT 6. tematický okruh: PLANIMETRIE vytvořila: RNDr. Věra Effenberger expertka na online přípravu na SMZ
Trojúhelník. MATEMATIKA pro 1. ročníky tříletých učebních oborů. Ing. Miroslav Čapek srpen 2011
 MATEMATIKA pro 1. ročníky tříletých učebních oborů Trojúhelník Ing. Miroslav Čapek srpen 2011 Projekt Využití e-learningu k rozvoji klíčových kompetencí reg. č.: CZ.1.07/1.1.10/03.0021 je spolufinancován
MATEMATIKA pro 1. ročníky tříletých učebních oborů Trojúhelník Ing. Miroslav Čapek srpen 2011 Projekt Využití e-learningu k rozvoji klíčových kompetencí reg. č.: CZ.1.07/1.1.10/03.0021 je spolufinancován
Máme tři různé body A, B, C. Trojúhelník ABC je průnik polorovin ABC, BCA a CAB.
 8. Trojúhelník 6. ročník 8. Trojúhelník 8.1. Základní pojmy 8.1.1. Trojúhelník Máme tři různé body A, B, C. Trojúhelník ABC je průnik polorovin ABC, BCA a CAB. Trojúhelník popisujeme proti chodu hodinových
8. Trojúhelník 6. ročník 8. Trojúhelník 8.1. Základní pojmy 8.1.1. Trojúhelník Máme tři různé body A, B, C. Trojúhelník ABC je průnik polorovin ABC, BCA a CAB. Trojúhelník popisujeme proti chodu hodinových
PLANIMETRIE, KONSTRUKČNÍ ÚLOHY V ROVINĚ
 PLANIMETRIE, KONSTRUKČNÍ ÚLOHY V ROVINĚ Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky
PLANIMETRIE, KONSTRUKČNÍ ÚLOHY V ROVINĚ Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky
February 05, Čtyřúhelníky lichoběžníky.notebook. 1. Vzdělávací oblast: Matematika a její aplikace
 Registrační číslo projektu: Název projektu: Název a číslo globálního grantu: CZ.1.07/1.1.12/02.0010 Šumavská škola = evropská škola Zvyšování kvality ve vzdělání v Plzeňském kraji CZ.1.07/1.1.12 Název
Registrační číslo projektu: Název projektu: Název a číslo globálního grantu: CZ.1.07/1.1.12/02.0010 Šumavská škola = evropská škola Zvyšování kvality ve vzdělání v Plzeňském kraji CZ.1.07/1.1.12 Název
Základy geometrie - planimetrie
 Základy geometrie - planimetrie Základní pojmy - bod (A, B, X, Y...), přímka ( p, q, a... ), rovina ( α, β, π... ) - nedefinují se Polopřímka: bod dělí přímku na dvě polopřímky opačně orientované značíme
Základy geometrie - planimetrie Základní pojmy - bod (A, B, X, Y...), přímka ( p, q, a... ), rovina ( α, β, π... ) - nedefinují se Polopřímka: bod dělí přímku na dvě polopřímky opačně orientované značíme
Digitální učební materiál
 Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuk prostřednictvím ICT Číslo a název šablon klíčové aktivit III/2 Inovace a zkvalitnění výuk prostřednictvím
Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuk prostřednictvím ICT Číslo a název šablon klíčové aktivit III/2 Inovace a zkvalitnění výuk prostřednictvím
6. Úhel a jeho vlastnosti
 6. Úhel a jeho vlastnosti 6.1 Úhel, osa úhlu 6.1.1 Úhel Úhel je část roviny ohraničená dvěma polopřímkami se společným počátkem. Polopřímkám říkáme ramena úhlu. Jejich společný počátek nazýváme vrchol
6. Úhel a jeho vlastnosti 6.1 Úhel, osa úhlu 6.1.1 Úhel Úhel je část roviny ohraničená dvěma polopřímkami se společným počátkem. Polopřímkám říkáme ramena úhlu. Jejich společný počátek nazýváme vrchol
ZÁKLADNÍ PLANIMETRICKÉ POJMY
 ZÁKLADNÍ PLANIMETRICKÉ POJMY Základní geometrické pojmy jsou bod, přímka a rovina. Geometrie je chápána jako část matematiky, která se zabývá studiem geometrických útvarů v rovině. Body určujeme jako průsečíky
ZÁKLADNÍ PLANIMETRICKÉ POJMY Základní geometrické pojmy jsou bod, přímka a rovina. Geometrie je chápána jako část matematiky, která se zabývá studiem geometrických útvarů v rovině. Body určujeme jako průsečíky
Základní geometrické tvary
 Základní geometrické tvary č. 37 Matematika 1. Narýsuj bod A. 2. Narýsuj přímku b. 3. Narýsuj přímku, která je dána body AB. AB 4. Narýsuj polopřímku CD. CD 5. Narýsuj úsečku AB. 6. Doplň. Rýsujeme v rovině.
Základní geometrické tvary č. 37 Matematika 1. Narýsuj bod A. 2. Narýsuj přímku b. 3. Narýsuj přímku, která je dána body AB. AB 4. Narýsuj polopřímku CD. CD 5. Narýsuj úsečku AB. 6. Doplň. Rýsujeme v rovině.
- shodnost trojúhelníků. Věta SSS: Věta SUS: Věta USU:
 1/12 PLANIMETRIE Základní pojmy: Shodnost, podobnost trojúhelníků Středová souměrnost, osová souměrnost, posunutí, otočení shodná zobrazení Středový a obvodový úhel Obsahy a obvody rovinných obrazců 1.
1/12 PLANIMETRIE Základní pojmy: Shodnost, podobnost trojúhelníků Středová souměrnost, osová souměrnost, posunutí, otočení shodná zobrazení Středový a obvodový úhel Obsahy a obvody rovinných obrazců 1.
GEODETICKÉ VÝPOČTY I.
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. TROJÚHELNÍK PYTHAGOROVA VĚTA TROJÚHELNÍK Geodetické výpočty I. trojúhelník je geometrický rovinný útvar určený třemi
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. TROJÚHELNÍK PYTHAGOROVA VĚTA TROJÚHELNÍK Geodetické výpočty I. trojúhelník je geometrický rovinný útvar určený třemi
Univerzita Karlova v Praze Pedagogická fakulta
 Univerzita Karlova v Praze Pedagogická fakulta SEMINÁRNÍ PRÁCE Z METOD ŘEŠENÍ 1 PLANIMETRIE 000/001 Cifrik, M-ZT První příklad ze zadávacích listů 1 Zadání: Sestrojte trojúhelník ABC, pokud je dáno: ρ
Univerzita Karlova v Praze Pedagogická fakulta SEMINÁRNÍ PRÁCE Z METOD ŘEŠENÍ 1 PLANIMETRIE 000/001 Cifrik, M-ZT První příklad ze zadávacích listů 1 Zadání: Sestrojte trojúhelník ABC, pokud je dáno: ρ
Sčítání a odčítání Jsou-li oba sčítanci kladní, znaménko výsledku je + +421 +23 = + 444
 ARITMETIKA CELÁ ČÍSLA Celá čísla jsou. -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, Celá čísla rozdělujeme na záporná (-1, -2, -3, ) kladná (1, 2, 3,.) nula 0 (není číslo kladné ani záporné) absolutní
ARITMETIKA CELÁ ČÍSLA Celá čísla jsou. -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, Celá čísla rozdělujeme na záporná (-1, -2, -3, ) kladná (1, 2, 3,.) nula 0 (není číslo kladné ani záporné) absolutní
Úvod. Cílová skupina: 2 Planimetrie
 PLANIMETRIE, KONSTRUKČNÍ ÚLOHY V ROVINĚ Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matemati ky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování
PLANIMETRIE, KONSTRUKČNÍ ÚLOHY V ROVINĚ Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matemati ky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování
Téma 5: PLANIMETRIE (úhly, vlastnosti rovinných útvarů, obsahy a obvody rovinných útvarů) Úhly 1) Jaká je velikost úhlu? a) 60 b) 80 c) 40 d) 30
 Téma 5: PLANIMETRIE (úhly, vlastnosti rovinných útvarů, obsahy a obvody rovinných útvarů) Úhly 1) Jaká je velikost úhlu? a) 60 b) 80 c) 40 d) 30 2) Vypočtěte velikost úhlu : a) 150 10 b) 149 22 c) 151
Téma 5: PLANIMETRIE (úhly, vlastnosti rovinných útvarů, obsahy a obvody rovinných útvarů) Úhly 1) Jaká je velikost úhlu? a) 60 b) 80 c) 40 d) 30 2) Vypočtěte velikost úhlu : a) 150 10 b) 149 22 c) 151
M - Planimetrie pro studijní obory
 M - Planimetrie pro studijní obory Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu je dovoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl
M - Planimetrie pro studijní obory Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu je dovoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl
Klíčová slova: Phytagorova věta, obsahy a obvody rovinných útvarů, úhlopříčky a jejich vlastnosti, úhly v rovinných útvarech, převody jednotek
 Přípravný kurz - Matematika Téma: Výpočtová geometrie v rovině Klíčová slova: Phytagorova věta, obsahy a obvody rovinných útvarů, úhlopříčky a jejich vlastnosti, úhly v rovinných útvarech, převody jednotek
Přípravný kurz - Matematika Téma: Výpočtová geometrie v rovině Klíčová slova: Phytagorova věta, obsahy a obvody rovinných útvarů, úhlopříčky a jejich vlastnosti, úhly v rovinných útvarech, převody jednotek
Klíčová slova: Phytagorova věta, obsahy a obvody rovinných útvarů, úhlopříčky a jejich vlastnosti, úhly v rovinných útvarech, převody jednotek
 Přípravný kurz - Matematika Téma: Výpočtová geometrie v rovině Klíčová slova: Phytagorova věta, obsahy a obvody rovinných útvarů, úhlopříčky a jejich vlastnosti, úhly v rovinných útvarech, převody jednotek
Přípravný kurz - Matematika Téma: Výpočtová geometrie v rovině Klíčová slova: Phytagorova věta, obsahy a obvody rovinných útvarů, úhlopříčky a jejich vlastnosti, úhly v rovinných útvarech, převody jednotek
Klíčová slova: Phytagorova věta, obsahy a obvody rovinných útvarů, úhlopříčky a jejich vlastnosti, úhly v rovinných útvarech, převody jednotek
 Přípravný kurz - Matematika Téma: Výpočtová geometrie v rovině Klíčová slova: Phytagorova věta, obsahy a obvody rovinných útvarů, úhlopříčky a jejich vlastnosti, úhly v rovinných útvarech, převody jednotek
Přípravný kurz - Matematika Téma: Výpočtová geometrie v rovině Klíčová slova: Phytagorova věta, obsahy a obvody rovinných útvarů, úhlopříčky a jejich vlastnosti, úhly v rovinných útvarech, převody jednotek
Syntetická geometrie I
 Shodnost Pedagogická fakulta 2018 www.karlin.mff.cuni.cz/~zamboj/ Vzdálenost dvou bodů Definice (Vzdálenost) Necht A, B, C ρ. Vzdálenost dvou bodů A, B v rovině je číslo AB a platí AB 0 AB = 0 A = B AB
Shodnost Pedagogická fakulta 2018 www.karlin.mff.cuni.cz/~zamboj/ Vzdálenost dvou bodů Definice (Vzdálenost) Necht A, B, C ρ. Vzdálenost dvou bodů A, B v rovině je číslo AB a platí AB 0 AB = 0 A = B AB
SHODNÁ ZOBRAZENÍ V ROVINĚ GEOMETRICKÁ ZOBRAZENÍ V ROVINĚ SHODNÁ ZOBRAZENÍ
 Předmět: Ročník: Vytvořil: Datum: MTEMTIK DRUHÝ Mgr. Tomáš MŇÁK 21. června 2012 Název zpracovaného celku: SHODNÁ ZORZENÍ V ROVINĚ Teoretická část GEOMETRICKÁ ZORZENÍ V ROVINĚ Zobrazení Z v rovině je předpis,
Předmět: Ročník: Vytvořil: Datum: MTEMTIK DRUHÝ Mgr. Tomáš MŇÁK 21. června 2012 Název zpracovaného celku: SHODNÁ ZORZENÍ V ROVINĚ Teoretická část GEOMETRICKÁ ZORZENÍ V ROVINĚ Zobrazení Z v rovině je předpis,
( ) ( ) 6. Algebraické nerovnice s jednou neznámou ( ) ( ) ( ) ( 2. e) = ( )
 6. Algebraické nerovnice s jednou neznámou Další dovednosti: -iracionální nerovnice -lineární nerovnice s parametrem -kvadratické nerovnice s parametrem Možné maturitní otázky: Lineární a kvadratické nerovnice
6. Algebraické nerovnice s jednou neznámou Další dovednosti: -iracionální nerovnice -lineární nerovnice s parametrem -kvadratické nerovnice s parametrem Možné maturitní otázky: Lineární a kvadratické nerovnice
Trojúhelník - určují tři body které neleţí na jedné přímce. Trojúhelník je rovněţ moţno povaţovat za průnik tří polorovin nebo tří konvexních úhlů.
 Trojúhelník Trojúhelník - určují tři body které neleţí na jedné přímce. Trojúhelník je rovněţ moţno povaţovat za průnik tří polorovin nebo tří konvexních úhlů. C Body se nazývají vrcholy trojúhelníku Úsečky
Trojúhelník Trojúhelník - určují tři body které neleţí na jedné přímce. Trojúhelník je rovněţ moţno povaţovat za průnik tří polorovin nebo tří konvexních úhlů. C Body se nazývají vrcholy trojúhelníku Úsečky
16. Trojúhelník vlastnosti, prvky, konstrukční úlohy Vypracovala: Ing. Ludmila Všetulová, prosinec 2013
 16. Trojúhelník vlastnosti, prvky, konstrukční úlohy Vypracovala: Ing. Ludmila Všetulová, prosinec 2013 Název školy Obchodní akademie a Střední odborné učiliště Veselí nad Moravou Název a číslo OP OP Vzdělávání
16. Trojúhelník vlastnosti, prvky, konstrukční úlohy Vypracovala: Ing. Ludmila Všetulová, prosinec 2013 Název školy Obchodní akademie a Střední odborné učiliště Veselí nad Moravou Název a číslo OP OP Vzdělávání
EU PENÍZE ŠKOLÁM Operační program Vzdělávání pro konkurenceschopnost
 ZÁKLADNÍ ŠKOLA OLOMOUC příspěvková organizace MOZARTOVA 48, 779 00 OLOMOUC tel.: 585 427 142, 775 116 442; fax: 585 422 713 e-mail: kundrum@centrum.cz; www.zs-mozartova.cz Projekt: ŠKOLA RADOSTI, ŠKOLA
ZÁKLADNÍ ŠKOLA OLOMOUC příspěvková organizace MOZARTOVA 48, 779 00 OLOMOUC tel.: 585 427 142, 775 116 442; fax: 585 422 713 e-mail: kundrum@centrum.cz; www.zs-mozartova.cz Projekt: ŠKOLA RADOSTI, ŠKOLA
SHODNÁ A PODOBNÁ ZOBRAZENÍ V ROVINĚ
 Technická univerzita v Liberci Fakulta přírodovědně-humanitní a pedagogická Katedra matematiky a didaktiky matematiky HODNÁ PODOBNÁ ZOBRZENÍ V ROVINĚ Pomocný učební text Petra Pirklová Liberec, září 2013
Technická univerzita v Liberci Fakulta přírodovědně-humanitní a pedagogická Katedra matematiky a didaktiky matematiky HODNÁ PODOBNÁ ZOBRZENÍ V ROVINĚ Pomocný učební text Petra Pirklová Liberec, září 2013
Shodné zobrazení v rovině
 Gymnázium Cheb Shodné zobrazení v rovině seminární práce Cheb, 2007 Lojza Tran Prohlášení Prohlašuji, že jsem seminární práci na téma: Shodné zobrazení v rovině vypracoval zcela sám za použití pramenů
Gymnázium Cheb Shodné zobrazení v rovině seminární práce Cheb, 2007 Lojza Tran Prohlášení Prohlašuji, že jsem seminární práci na téma: Shodné zobrazení v rovině vypracoval zcela sám za použití pramenů
Shodná zobrazení v rovině
 Shodná zobrazení v rovině Zobrazení Z v rovině je předpis, který každému bodu X roviny přiřazuje právě jeden bod X roviny. Bod X se nazývá vzor, bod X jeho obraz. Zapisujeme Z: X X. Množinu obrazů všech
Shodná zobrazení v rovině Zobrazení Z v rovině je předpis, který každému bodu X roviny přiřazuje právě jeden bod X roviny. Bod X se nazývá vzor, bod X jeho obraz. Zapisujeme Z: X X. Množinu obrazů všech
MATEMATIKA. Problémy a úlohy, v nichž podrobujeme geometrický objekt nějaké transformaci
 MATEMATIKA Úloha o čtverci a přímkách ŠÁRKA GERGELITSOVÁ TOMÁŠ HOLAN Matematicko-fyzikální fakulta UK, Praha Problémy a úlohy, v nichž podrobujeme geometrický objekt nějaké transformaci (například podobnosti)
MATEMATIKA Úloha o čtverci a přímkách ŠÁRKA GERGELITSOVÁ TOMÁŠ HOLAN Matematicko-fyzikální fakulta UK, Praha Problémy a úlohy, v nichž podrobujeme geometrický objekt nějaké transformaci (například podobnosti)
Obrázek 13: Plán starověké Alexandrie,
 4 Geometrické útvary v rovině Obrázek 13: Plán starověké Alexandrie, https://commons.wikimedia.org Jestliže rovinu chápeme jako množinu bodů, potom uvažované geometrické útvary jsou jejími podmnožinami.
4 Geometrické útvary v rovině Obrázek 13: Plán starověké Alexandrie, https://commons.wikimedia.org Jestliže rovinu chápeme jako množinu bodů, potom uvažované geometrické útvary jsou jejími podmnožinami.
Užití stejnolehlosti v konstrukčních úlohách
 Užití stejnolehlosti v konstrukčních úlohách Příklad 1: Je dána kružnice k(o,r) a bod M ležící uvnitř kružnice k. Bodem M veďte tětivu AB, jejíž délka je bodem M rozdělena v poměru 2 : 1. Sestrojte obraz
Užití stejnolehlosti v konstrukčních úlohách Příklad 1: Je dána kružnice k(o,r) a bod M ležící uvnitř kružnice k. Bodem M veďte tětivu AB, jejíž délka je bodem M rozdělena v poměru 2 : 1. Sestrojte obraz
Předmět: Ročník: Vytvořil: Datum: MATEMATIKA DRUHÝ MGR. JÜTTNEROVÁ Název zpracovaného celku: PODOBNOST A STEJNOLEHLOST PODOBNOST
 Předmět: Ročník: Vytvořil: Datum: MATEMATIKA DRUHÝ MGR. JÜTTNEROVÁ 7. 5. 0 Název zpracovaného celku: PODOBNOST A STEJNOLEHLOST PODOBNOST Je každé zobrazení v rovině takové, že pro libovolné body roviny
Předmět: Ročník: Vytvořil: Datum: MATEMATIKA DRUHÝ MGR. JÜTTNEROVÁ 7. 5. 0 Název zpracovaného celku: PODOBNOST A STEJNOLEHLOST PODOBNOST Je každé zobrazení v rovině takové, že pro libovolné body roviny
Pracovní listy MONGEOVO PROMÍTÁNÍ
 Technická univerzita v Liberci Fakulta přírodovědně-humanitní a pedagogická Katedra matematiky a didaktiky matematiky MONGEOVO PROMÍTÁNÍ Petra Pirklová Liberec, únor 07 . Zobrazte tyto body a určete jejich
Technická univerzita v Liberci Fakulta přírodovědně-humanitní a pedagogická Katedra matematiky a didaktiky matematiky MONGEOVO PROMÍTÁNÍ Petra Pirklová Liberec, únor 07 . Zobrazte tyto body a určete jejich
ICT podporuje moderní způsoby výuky CZ.1.07/1.5.00/ Matematika planimetrie. Mgr. Tomáš Novotný
 Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity IV/2 Inovace
Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity IV/2 Inovace
9. Planimetrie 1 bod
 9. Plnimetrie 1 bod 9.1. Do rovnostrnného trojúhelníku ABC o strně je vepsán rovnostrnný trojúhelník DEF tk, že D AB, E BC, F CA. Jestliže obsh trojúhelníku DEF je roven polovině obshu trojúhelníku ABC,
9. Plnimetrie 1 bod 9.1. Do rovnostrnného trojúhelníku ABC o strně je vepsán rovnostrnný trojúhelník DEF tk, že D AB, E BC, F CA. Jestliže obsh trojúhelníku DEF je roven polovině obshu trojúhelníku ABC,
Kapitola 5. Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které
 Kapitola 5 Kuželosečky Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které společně s kružnicí jsou známy pod společným názvem kuželosečky. Říká se jim tak proto, že každou z nich
Kapitola 5 Kuželosečky Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které společně s kružnicí jsou známy pod společným názvem kuželosečky. Říká se jim tak proto, že každou z nich
SHODNÁ ZOBRAZENÍ V ROVINĚ
 Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol SHODNÁ
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol SHODNÁ
Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Přírodovědné
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Přírodovědné
Syntetická geometrie II
 Mnohoúhelníky Pedagogická fakulta 2018 www.karlin.mff.cuni.cz/~zamboj/ Čtyřúhelníky Definice (Čtyřúhelník) Jsou dány čtyři body A, B, C, D v rovině, z nichž žádné tři nejsou kolineární. Čtyřúhelník ABCD
Mnohoúhelníky Pedagogická fakulta 2018 www.karlin.mff.cuni.cz/~zamboj/ Čtyřúhelníky Definice (Čtyřúhelník) Jsou dány čtyři body A, B, C, D v rovině, z nichž žádné tři nejsou kolineární. Čtyřúhelník ABCD
Syntetická geometrie I
 Shodnost Pedagogická fakulta 2016 www.karlin.mff.cuni.cz/~zamboj/ Vzdálenost dvou bodů Necht A, B, C ρ. Vzdálenost dvou bodů A, B v rovině je číslo AB a platí AB 0 AB = 0 A = B AB = BA pozitivně definitní
Shodnost Pedagogická fakulta 2016 www.karlin.mff.cuni.cz/~zamboj/ Vzdálenost dvou bodů Necht A, B, C ρ. Vzdálenost dvou bodů A, B v rovině je číslo AB a platí AB 0 AB = 0 A = B AB = BA pozitivně definitní
M - Pythagorova věta, Eukleidovy věty
 M - Pythagorova věta, Eukleidovy věty Určeno jako učební text pro studenty dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací
M - Pythagorova věta, Eukleidovy věty Určeno jako učební text pro studenty dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací
Projekt: ŠKOLA RADOSTI, ŠKOLA KVALITY Registrační číslo projektu: CZ.1.07/1.4.00/ EU PENÍZE ŠKOLÁM
 ZÁKLDNÍ ŠKOL OLOMOU příspěvková organizace MOZRTOV 48, 779 00 OLOMOU tel.: 585 427 142, 775 116 442; fax: 585 422 713 email: kundrum@centrum.cz; www.zs-mozartova.cz Projekt: ŠKOL RDOSTI, ŠKOL KVLITY Registrační
ZÁKLDNÍ ŠKOL OLOMOU příspěvková organizace MOZRTOV 48, 779 00 OLOMOU tel.: 585 427 142, 775 116 442; fax: 585 422 713 email: kundrum@centrum.cz; www.zs-mozartova.cz Projekt: ŠKOL RDOSTI, ŠKOL KVLITY Registrační
GEOMETRIE. Projekt byl podpořen z Evropského sociálního fondu. Praha & EU: Investujeme do vaší budoucnosti
 GEOMETRIE pracovní sešit pro 6. ročník Projekt byl podpořen z Evropského sociálního fondu. Praha & EU: Investujeme do vaší budoucnosti Tato publikace byla vytvořena v souladu s RVP ZV v rámci projektu
GEOMETRIE pracovní sešit pro 6. ročník Projekt byl podpořen z Evropského sociálního fondu. Praha & EU: Investujeme do vaší budoucnosti Tato publikace byla vytvořena v souladu s RVP ZV v rámci projektu
A STEJNOLEHLOST,, EUKLIDOVYE VĚTY 2.
 PODOBNOST A STEJNOLEHLOST,, EUKLIDOVYE VĚTY 2. ČÁST MAT. OT 2. OT. Č.. 15: SHODNÁS HODNÁ ZOBRAZENÍ V ROVINĚ, PODOBNOST A STEJNOLEHLOST,, EUKLIDOVYE VĚTY PODOBNOST KDE LÁTKU NAJDETE Kapitola Základy planimetrie
PODOBNOST A STEJNOLEHLOST,, EUKLIDOVYE VĚTY 2. ČÁST MAT. OT 2. OT. Č.. 15: SHODNÁS HODNÁ ZOBRAZENÍ V ROVINĚ, PODOBNOST A STEJNOLEHLOST,, EUKLIDOVYE VĚTY PODOBNOST KDE LÁTKU NAJDETE Kapitola Základy planimetrie
8 Podobná (ekviformní) zobrazení v rovině
 Typeset by LATEX2ε 1 8 Podobná (ekviformní) zobrazení v rovině 8.1 Stejnolehlost (homotetie) v rovině Definice 8.1.1. Nechť jsou dány 3 různé kolineární body A, B, C. Dělicím poměrem λ = (ABC) rozumíme
Typeset by LATEX2ε 1 8 Podobná (ekviformní) zobrazení v rovině 8.1 Stejnolehlost (homotetie) v rovině Definice 8.1.1. Nechť jsou dány 3 různé kolineární body A, B, C. Dělicím poměrem λ = (ABC) rozumíme
Planimetrie úvod, základní pojmy (teorie)
 Planimetrie úvod, základní pojmy (teorie) Geometrie (původně zeměměřictví) nyní část matematiky, zabývající se studiem geometrických objektů Planimetrie rovinná geometrie Stereometrie prostorová geometrie
Planimetrie úvod, základní pojmy (teorie) Geometrie (původně zeměměřictví) nyní část matematiky, zabývající se studiem geometrických objektů Planimetrie rovinná geometrie Stereometrie prostorová geometrie
Planimetrie. Příklad 1. Zapište vztahy mezi body a přímkami, které jsou vyznačeny na obrázku. Příklad 2. Určete body K, L, M pomocí přímek p, r, s.
 Planimetrie Část matematiky, zabývající se studiem rovinných geometrických objekt (rovinná geometrie). bstrakcí z hmotných objektů vznikly základní geometrické pojmy bod přímka Bod Body označujeme velkými
Planimetrie Část matematiky, zabývající se studiem rovinných geometrických objekt (rovinná geometrie). bstrakcí z hmotných objektů vznikly základní geometrické pojmy bod přímka Bod Body označujeme velkými
PODOBNÁ ZOBRAZENÍ V ROVINĚ (včetně stejnolehlosti)
 Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol PODOBNÁ
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol PODOBNÁ
A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz
![A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz](/thumbs/47/23721460.jpg) 1/15 ANALYTICKÁ GEOMETRIE Základní pojmy: Soustava souřadnic v rovině a prostoru Vzdálenost bodů, střed úsečky Vektory, operace s vektory, velikost vektoru, skalární součin Rovnice přímky Geometrie v rovině
1/15 ANALYTICKÁ GEOMETRIE Základní pojmy: Soustava souřadnic v rovině a prostoru Vzdálenost bodů, střed úsečky Vektory, operace s vektory, velikost vektoru, skalární součin Rovnice přímky Geometrie v rovině
AXONOMETRIE. Rozměry ve směru os (souřadnice bodů) jsou násobkem příslušné jednotky.
 AXONOMETRIE 1) Princip, základní pojmy Axonometrie je rovnoběžné promítání do průmětny různoběžné se souřadnicovými rovinami. Kvádr v axonometrii : {O,x,y,z} souřadnicový systém XYZ - axonometrická průmětna
AXONOMETRIE 1) Princip, základní pojmy Axonometrie je rovnoběžné promítání do průmětny různoběžné se souřadnicovými rovinami. Kvádr v axonometrii : {O,x,y,z} souřadnicový systém XYZ - axonometrická průmětna
Mgr. Monika Urbancová. a vepsané trojúhelníku
 Název projektu Život jako leporelo Registrační číslo CZ.1.07/1.4.00/21.3763 Autor Mgr. Monika Urbancová Datum 28. 8. 2014 Ročník 6. ročník Vzdělávací oblast MATEMATIKA A JEJÍ APLIKACE Vzdělávací obor MATEMATIKA
Název projektu Život jako leporelo Registrační číslo CZ.1.07/1.4.00/21.3763 Autor Mgr. Monika Urbancová Datum 28. 8. 2014 Ročník 6. ročník Vzdělávací oblast MATEMATIKA A JEJÍ APLIKACE Vzdělávací obor MATEMATIKA
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Přírodovědné
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Přírodovědné
10)(- 5) 2 = 11) 5 12)3,42 2 = 13)380 2 = 14)4, = 15) = 16)0, = 17)48,69 2 = 18) 25, 23 10) 12) ) )
 Druhá mocnina z tabulek 1) (- 6) = 10)(- 5) = ) 7 = 4 11) 5 = ) 4,8 = 4) 40 = 5),785 = 6) 65 8 = 7) 0,01485 = 8) 5,7 = 9) = 4 1),4 = 1)80 = 14)4,6787 = 15)467 56 = 16)0,014 = 17)48,69 = 1 18) Druhá odmocnina
Druhá mocnina z tabulek 1) (- 6) = 10)(- 5) = ) 7 = 4 11) 5 = ) 4,8 = 4) 40 = 5),785 = 6) 65 8 = 7) 0,01485 = 8) 5,7 = 9) = 4 1),4 = 1)80 = 14)4,6787 = 15)467 56 = 16)0,014 = 17)48,69 = 1 18) Druhá odmocnina
prostorová definice (viz obrázek vlevo nahoře): elipsa je průsečnou křivkou rovinného
 Elipsa Výklad efinice a ohniskové vlastnosti prostorová definice (viz obrázek vlevo nahoře): elipsa je průsečnou křivkou rovinného řezu na rotační kuželové ploše, jestliže řezná rovina není kolmá k ose
Elipsa Výklad efinice a ohniskové vlastnosti prostorová definice (viz obrázek vlevo nahoře): elipsa je průsečnou křivkou rovinného řezu na rotační kuželové ploše, jestliže řezná rovina není kolmá k ose
Základní úlohy v Mongeově promítání. n 2 A 1 A 1 A 1. p 1 N 2 A 2. x 1,2 N 1 x 1,2. x 1,2 N 1
 Základní úlohy v Mongeově promítání Předpokladem ke zvládnutí zobrazení v Mongeově promítání je znalost základních úloh. Ale k porozumění následujícího textu je třeba umět zobrazit bod, přímku a rovinu
Základní úlohy v Mongeově promítání Předpokladem ke zvládnutí zobrazení v Mongeově promítání je znalost základních úloh. Ale k porozumění následujícího textu je třeba umět zobrazit bod, přímku a rovinu
Vlasta Moravcová. Matematicko-fyzikální fakulta & Nad Ohradou 23 Univerzita Karlova v Praze Praha 3. Letní škola geometrie 2018,
 KONSTRUKČNÍ ÚLOHY Katedra didaktiky matematiky Gymnázium Na Pražačce Matematicko-fyzikální fakulta & Nad Ohradou 23 Univerzita Karlova v Praze Praha 3 Letní škola geometrie 2018, 4. července 2018, Česká
KONSTRUKČNÍ ÚLOHY Katedra didaktiky matematiky Gymnázium Na Pražačce Matematicko-fyzikální fakulta & Nad Ohradou 23 Univerzita Karlova v Praze Praha 3 Letní škola geometrie 2018, 4. července 2018, Česká
z přímek a kružnic 35. Čtverec s danou stranou: 1. Oblouky A-B, B-A (přímka CED); 2. Oblouk E-AB (F); 3. Přímky AF, BF a vzniklé průsečíky
 ČTVERCE A KOSOčTVERCE z přímek a kružnic Jednoduché čtyřúhelníkové konstrukce se dají zvládnout snadno. Abyste sestrojili kružnici opsanou čtverci nebo obdélníku, nejprve zakreslete úhlopříčky a pak narýsujte
ČTVERCE A KOSOčTVERCE z přímek a kružnic Jednoduché čtyřúhelníkové konstrukce se dají zvládnout snadno. Abyste sestrojili kružnici opsanou čtverci nebo obdélníku, nejprve zakreslete úhlopříčky a pak narýsujte
2) Přednáška trvala 80 minut a skončila v 17:35. Jirka na ni přišel v 16:20. Kolik úvodních minut přednášky Jirka
 Téma 4: (převody jednotek, funkce, konstrukční úlohy, osová a středová souměrnost) Převody jednotek 1) Kolik gramů je pět třetin z 2,1 kilogramu? a) 1 260 g b) 3 500 g c) 17 000 g d) 700 g 2) Přednáška
Téma 4: (převody jednotek, funkce, konstrukční úlohy, osová a středová souměrnost) Převody jednotek 1) Kolik gramů je pět třetin z 2,1 kilogramu? a) 1 260 g b) 3 500 g c) 17 000 g d) 700 g 2) Přednáška
Planimetrie pro studijní obory
 Variace 1 Planimetrie pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Planimetrie Planimetrie
Variace 1 Planimetrie pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Planimetrie Planimetrie
EU PENÍZE ŠKOLÁM Operační program Vzdělávání pro konkurenceschopnost
 ZÁKLADNÍ ŠKOLA OLOMOUC příspěvková organizace MOZARTOVA 48, 779 00 OLOMOUC tel.: 585 427 142, 775 116 442; fax: 585 422 713 e-mail: kundrum@centrum.cz; www.zs-mozartova.cz Projekt: ŠKOLA RADOSTI, ŠKOLA
ZÁKLADNÍ ŠKOLA OLOMOUC příspěvková organizace MOZARTOVA 48, 779 00 OLOMOUC tel.: 585 427 142, 775 116 442; fax: 585 422 713 e-mail: kundrum@centrum.cz; www.zs-mozartova.cz Projekt: ŠKOLA RADOSTI, ŠKOLA
Syntetická geometrie I
 Kružnice Pedagogická fakulta 2016 www.karlin.mff.cuni.cz/~zamboj/ & přímka Vzájemná poloha přímky a kružnice p 1 vnější přímka p 2 tečna s bodem dotyku T p 3 sečna X 1 X 2 tětiva Y 1 Y 2 průměr Y 1 S poloměr
Kružnice Pedagogická fakulta 2016 www.karlin.mff.cuni.cz/~zamboj/ & přímka Vzájemná poloha přímky a kružnice p 1 vnější přímka p 2 tečna s bodem dotyku T p 3 sečna X 1 X 2 tětiva Y 1 Y 2 průměr Y 1 S poloměr
Syntetická geometrie I
 Kružnice Pedagogická fakulta 2018 www.karlin.mff.cuni.cz/~zamboj/ & přímka Vzájemná poloha přímky a kružnice p 1 vnější přímka p 2 tečna s bodem dotyku T p 3 sečna X 1 X 2 tětiva Y 1 Y 2 průměr Y 1 S poloměr
Kružnice Pedagogická fakulta 2018 www.karlin.mff.cuni.cz/~zamboj/ & přímka Vzájemná poloha přímky a kružnice p 1 vnější přímka p 2 tečna s bodem dotyku T p 3 sečna X 1 X 2 tětiva Y 1 Y 2 průměr Y 1 S poloměr
Trojúhelník. Jan Kábrt
 Trojúhelník Jan Kábrt Co se učívá ve školách Výšky, jejich průsečík ortocentrum O Těžnice, jejich průsečík těžiště T Osy stran, střed kružnice opsané S o Osy úhlů, střed kružnice vepsané S v Někdy ještě
Trojúhelník Jan Kábrt Co se učívá ve školách Výšky, jejich průsečík ortocentrum O Těžnice, jejich průsečík těžiště T Osy stran, střed kružnice opsané S o Osy úhlů, střed kružnice vepsané S v Někdy ještě
16. žákcharakterizujeatřídízákladnírovinnéútvary
 OČEKÁVANÝ VÝSTUP PODLE RVP ZV 1. žákcharakterizujeatřídízákladnírovinnéútvary Úloha 1 Rovinné útvary v obrázku jsou označeny symboly A L. A B C D E F G H I J K L V tabulce je uveden název obrazce a odpovídající
OČEKÁVANÝ VÝSTUP PODLE RVP ZV 1. žákcharakterizujeatřídízákladnírovinnéútvary Úloha 1 Rovinné útvary v obrázku jsou označeny symboly A L. A B C D E F G H I J K L V tabulce je uveden název obrazce a odpovídající
Úlohy domácí části I. kola kategorie C
 63. ročník Matematické olympiády Úlohy domácí části I. kola kategorie C 1. Určete, jaké nejmenší hodnoty může nabýt výraz V = (a b) + (b c) + (c a), splňují-li reálná čísla a, b, c dvojici podmínek a +
63. ročník Matematické olympiády Úlohy domácí části I. kola kategorie C 1. Určete, jaké nejmenší hodnoty může nabýt výraz V = (a b) + (b c) + (c a), splňují-li reálná čísla a, b, c dvojici podmínek a +
Test Zkušební přijímací zkoušky
 Test Zkušební přijímací zkoušky 1. Vypočtěte: ( 10 1.5) ( 4 ).( 15). ( 5 6). Doplňte číslo do rámečku, aby platila rovnost:.1. 4 11 10. 8 16 6.. 49 7 1.. + 1. Proveďte početní operace:.1. 6x 4x ( 4x x)
Test Zkušební přijímací zkoušky 1. Vypočtěte: ( 10 1.5) ( 4 ).( 15). ( 5 6). Doplňte číslo do rámečku, aby platila rovnost:.1. 4 11 10. 8 16 6.. 49 7 1.. + 1. Proveďte početní operace:.1. 6x 4x ( 4x x)
6. Čtyřúhelníky, mnohoúhelníky, hranoly
 6. Čtyřúhelníky, mnohoúhelníky, hranoly 7. ročník - 6. Čtyřúhelníky, mnohoúhelníky, hranoly 6.1. Základní pojmy 6.1.1. n úhelník n - úhelník pro n > 2 je geometrický obrazec, který má n vrcholů ( stran,
6. Čtyřúhelníky, mnohoúhelníky, hranoly 7. ročník - 6. Čtyřúhelníky, mnohoúhelníky, hranoly 6.1. Základní pojmy 6.1.1. n úhelník n - úhelník pro n > 2 je geometrický obrazec, který má n vrcholů ( stran,
PLANIMETRIE. Mgr. Zora Hauptová TROJÚHELNÍK VY_32_INOVACE_MA_1_04
 PLANIMETRIE Mgr. Zora Hauptová TROJÚHELNÍK VY_32_INOVACE_MA_1_04 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti Název školy Název šablony Předmět Tematický celek
PLANIMETRIE Mgr. Zora Hauptová TROJÚHELNÍK VY_32_INOVACE_MA_1_04 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti Název školy Název šablony Předmět Tematický celek
p ACD = 90, AC = 7,5 cm, CD = 12,5 cm
 Úloha Je dán pravoúhlý trojúhelník ACD s pravým úhlem při vrcholu C, AC = 7,5 cm, CD =,5 cm. Na přímce CD určete bod B tak, aby AB = BD Řešení: Úlohu vyřešíme nejprve geometrickou konstrukcí. a) Z rozboru
Úloha Je dán pravoúhlý trojúhelník ACD s pravým úhlem při vrcholu C, AC = 7,5 cm, CD =,5 cm. Na přímce CD určete bod B tak, aby AB = BD Řešení: Úlohu vyřešíme nejprve geometrickou konstrukcí. a) Z rozboru
je-li dáno: a) a = 4,6 cm; α = 28 ; b) b = 8,4 cm; β = 64. Při výpočtu nepoužívejte Pythagorovu větu!
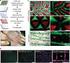 -----Pravoúhlý trojúhelník----- 156 V pravoúhlém trojúhelníku ABC má pravý úhel vrchol C. Vypočítejte velikost jeho ostrých úhlů, je-li dáno: a) a = 62 mm, b = 37 mm, b) a = 36 mm, c = 58 mm, c) b = 8,4
-----Pravoúhlý trojúhelník----- 156 V pravoúhlém trojúhelníku ABC má pravý úhel vrchol C. Vypočítejte velikost jeho ostrých úhlů, je-li dáno: a) a = 62 mm, b = 37 mm, b) a = 36 mm, c = 58 mm, c) b = 8,4
ÚVOD... 5 CÍLE PŘEDMĚTU... 7 1. ROVINNÉ ÚTVARY... 9 1.1. ZÁKLADNÍ PLANIMETRICKÉ POJMY... 10 ZNAČENÍ A ZÁPIS ZÁKLADNÍCH PLANIMETRICKÝCH ÚTVARŮ...
 O B C H O D N Í A K A D E M I E O R L O V Á M A T E M A T I K A I II Z Á K L A D Y G E O M E T R I E U Č E B N Í T E X T P R O D I S T A N Č N Í F O R M U V Z D Ě L Á V Á N Í E V A B A R T O Ň O V Á P
O B C H O D N Í A K A D E M I E O R L O V Á M A T E M A T I K A I II Z Á K L A D Y G E O M E T R I E U Č E B N Í T E X T P R O D I S T A N Č N Í F O R M U V Z D Ě L Á V Á N Í E V A B A R T O Ň O V Á P
Řešení geometrické úlohy spočívá v nalezení geometrického útvaru (útvarů) daných vlastností.
 Řešení geometrické úlohy spočívá v nalezení geometrického útvaru (útvarů) daných vlastností. Metody řešení konstrukčních úloh: množinou bodů zobrazením výpočtem kombinací předchozích způsobů Konstrukční
Řešení geometrické úlohy spočívá v nalezení geometrického útvaru (útvarů) daných vlastností. Metody řešení konstrukčních úloh: množinou bodů zobrazením výpočtem kombinací předchozích způsobů Konstrukční
3.1.2 Polorovina, úhel
 3.1.2 Polorovina, úhel Předpoklady: 3101 Přímka dělí rovinu na dvě navzájem opačné poloroviny a je jejich společnou hranicí (hraniční přímkou). p Hraniční přímka patří do obou polorovin. ody, které neleží
3.1.2 Polorovina, úhel Předpoklady: 3101 Přímka dělí rovinu na dvě navzájem opačné poloroviny a je jejich společnou hranicí (hraniční přímkou). p Hraniční přímka patří do obou polorovin. ody, které neleží
Deskriptivní geometrie 2
 Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra matematiky Deskriptivní geometrie 2 Pomocný učební text - díl II Světlana Tomiczková Plzeň 4. května 2011 verze 1.0 Obsah 1 Středové promítání
Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra matematiky Deskriptivní geometrie 2 Pomocný učební text - díl II Světlana Tomiczková Plzeň 4. května 2011 verze 1.0 Obsah 1 Středové promítání
MASARYKOVA UNIVERZITA. Čtyřúhelníky PEDAGOGICKÁ FAKULTA. Diplomová práce. Katedra matematiky. Brno Vedoucí práce: RNDr. Růžena Blažková, CSc.
 MASARYKOVA UNIVERZITA PEDAGOGICKÁ FAKULTA Katedra matematiky Čtyřúhelníky Diplomová práce Brno 2008 Vedoucí práce: RNDr. Růžena Blažková, CSc. Autor práce: Mgr. Marta Mrázová 1 Prohlášení Prohlašuji, že
MASARYKOVA UNIVERZITA PEDAGOGICKÁ FAKULTA Katedra matematiky Čtyřúhelníky Diplomová práce Brno 2008 Vedoucí práce: RNDr. Růžena Blažková, CSc. Autor práce: Mgr. Marta Mrázová 1 Prohlášení Prohlašuji, že
