Vlastní čísla a vlastní vektory
|
|
|
- Sabina Hrušková
- před 8 lety
- Počet zobrazení:
Transkript
1 Kapitola 11 Vlastní čísla a vlastní vektory Základní motivace pro studium vlastních čísel a vektorů pochází z teorie řešení diferenciálních rovnic Tato teorie říká, že obecné řešení lineární diferenciální rovnice u = λu, kde u(t) je neznámá reálná funkce reálné proměnné t, je tvaru u(t) = αe λt, kde α je reálné číslo Podobně soustava lineárních diferenciálních rovnic má řešení ve tvaru u 1 = 7u 1 4u 2 u 2 = 5u 1 2u 2 u 1 = α 1 e λt, u 2 = α 2 e λt pro vhodná reálná čísla α 1, α 2, λ Pokud tato vyjádření zderivujeme podle t a dosadíme do původní soustavy diferenciálních rovnic, dostaneme tj α 1 λe λt = 7α 1 e λt 4α 2 e λt α 2 λe λt = 5α 1 e λt 2α 2 e λt, α 1 λ = 7α 1 4α 2 α 2 λ = 5α 1 2α 2, neboli ( ) ( α1 α 2 1 ) = λ ( α1 α 2 )
2 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 2 V maticovém tvaru můžeme tuto soustavu vyjádřit jako ( ) 7 4 Ax = λx, kde A = a x = 5 2 ( α1 α 2 ) Tato soustava má triviální řešení x = 0, které pro libovolné λ vede k nulovým funkcím u 1, u 2 To není příliš zajímavé řešení Zajímají nás spíš ty hodnoty skaláru λ, pro které existuje nenulové řešení soustavy Ax = λx, tj soustavy (A λi)x = 0 Nenulové řešení existuje právě když je matice A λi singulární, tj právě když det(a λi) = 0 Nenulové řešení proto existuje pouze pro hodnoty λ vyhovující kvadratické rovnici tj (7 λ)( 2 λ) + 20 = 0, λ 2 5λ + 6 = 0 Tato kvadratická rovnice má řešení λ = 2 a λ = 3 Pro λ = 2 hledáme řešení homogenní soustavy s maticí ( ) 5 4 A 2I =, 5 4 která má řešení tvaru x = a(4/5, 1) T Hodnota λ = 2 tak vede k následujícímu řešení původní soustavy diferfenciálních rovnic ( ) ( ) u1 u 1 = = e 2t 4/5 1 u 2 Druhé řešení kvadratické rovnice λ = 3 vede k homogenní soustavě s maticí ( ) 4 4 A 3I =, 5 5 která má řešení x = b(1, 1) T Hodnota λ = 3 pak vede k řešení u 2 = ( u1 u 2 ) = e 3t ( 1 1 Lze dokázat, že každé řešení původní soustavy diferenciálních rovnic u = Au je lineární kombinací těchto dvou řešení u 1 a u 2 Uvedená úloha vede k následující definici )
3 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 3 Definice 111 Pro čtvercovou matici A řádu n s reálnými (komplexními) prvky definujeme vlastní číslo matice A jako komplexní číslo λ, pro které platí Ax = λx pro nějaký nenulový vektor x R n 1 (C n 1 ) Je-li λ vlastní číslo matice A, pak každé řešení soustavy lineárních rovnic (A λi n )x = 0 nazýváme vlastní vektor matice A příslušný vlastnímu číslu λ Množinu všech vlastních čísel matice A nazýváme spektrum matice A a označujeme ji σ(a) Z definice tak přímo plyne, že pro komplexní matici A řádu n a komplexní číslo λ platí λ σ(a) právě když matice A λi n je singulární, což je právě když det(a λi n ) = 0 Poslední podmínka říká, jak najít vlastní čísla nějaké matice, pokud existují Definice 112 Je-li A čtvercová matice řádu n s reálnými (komplexními) prvky, pak pro každé reálné (komplexní) číslo λ definujeme hodnotu p(λ) = det(a λi n ) Funkci p(λ) nazýváme charakteristický polynom matice A Rovnici p(λ) = 0 nazýváme charakteristická rovnice matice A Pro důkaz Tvrzení 114 budeme potřebovat následující obecnou větu, které se říká základní věta algebry Její důkaz je hodně obtížný a překračuje rámec úvodního kurzu lineární algebry Uvedeme si ji proto bez důkazu Věta 113 Je-li f(x) = b n x n + b n 1 x n b 1 x + b 0 polynom stupně n 1 s komplexními koeficienty, pak jej lze vyjádřit ve tvaru f(x) = b n (x β 1 ) l 1 (x β 2 ) l2 (x β k ) l k, pro nějaká komplexní čísla β 1,, β k a kladná celá čísla l 1,, l k, pro která platí l 1 + l l k = n Čísla β 1,, β k se nazývají kořeny polynomu f, číslo l i se nazývá násobnost kořenu β i Tvrzení 114 Pro komplexní čtvercovou matici A = (a ij ) řádu n platí charakteristický polynom matice A řádu n je polynom stupně n s vedoucím koeficientem rovným ( 1) n, komplexní číslo λ je vlastním čísla matice A právě když je kořenem charakteristického polynomu p(λ) matice A, matice A má n vlastních komplexních čísel, počítáme-li každé tolikrát, kolik je jeho násobnost jako kořene charakteristického polynomu,
4 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 4 pokud je A reálná matice, pak λ σ(a) právě když λ σ(a) Důkaz První tvrzení vyplývá z definice determinantu Platí a 11 λ a 12 a 1n a 21 a 22 λ a 2n A λi n = a n1 a n2 a nn λ Vyjdeme-li z definice determinantu, je především je zřejmé, že determinant matice A λi n je polynom v proměnné λ V součinu diagonálních prvků (odpovídajícímu identické permutaci) (a 11 λ)(a 22 λ) (a nn λ) dostaneme po roznásobení, že koeficient u λ n je ( 1) n a koeficient u λ n 1 je ( 1) n 1 n i=1 a ii V jakémkoliv jiném součinu odpovídajícím neidentické permutaci p S n se musí objevit dva prvky mimo hlavní diagonálu, po případném roznásobení se tak může objevit neznámá λ s koeficientem nejvýše n 2 Proto je koeficient u λ n v charakteristickém polynomu matice A roven ( 1) n a koeficient u λ n 1 se rovná ( 1) n 1 n i=1 a ii Podobně můžete najít koeficienty u každé mocniny λ n k pro k = 2, 3,, n Druhé tvrzení plyne přímo z definice vlastního čísla a charakteristického polynomu Třetí tvrzení plyne zase ze základní věty algebry Čtvrté tvrzení plyne z toho, že je-li p(λ) = b n λ n +b n 1 λ n 1 + +b 1 λ 1 + b 0 = 0 a koeficienty b 0, b 1,, b n polynomu p jsou reálná čísla, pak rovněž p(λ) = b n λ n + b n 1 λ n b 1 λ + b 0 = 0 Je-li tedy λ vlastní číslo reálné matice, pak také λ je vlastní číslo této matice Každé vlastní číslo λ matice A je kořenem charakteristického polynomu p(λ) matice A a má tedy nějakou násobnost coby kořen polynomu p(λ) Tuto násobnost budeme rovněž nazývat algebraická násobnost charakteristického čísla λ, případně algebraická dimenze charakteristického čísla λ Reálná matice nemusí mít žádné reálné vlastní číslo Pokud je ale navíc symetrická, pak je každé vlastní číslo této matice reálné Podobné tvrzení platí i pro hermitovské matice, tj pro matice s komplexními prvky, pro které platí B = B
5 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 5 Tvrzení 115 Je-li A reálná symetrická matice, pak každé vlastní číslo matice A je reálné Podobně, je-li B hermitovská matice, pak každé vlastní číslo matice B je reálné Důkaz Důkaz stačí provést pro hermitovské matice, neboť každá symetrická matice je hermitovská Je-li λ σ(b) a x 0 vlastní vektor příslušný vlastnímu číslu λ, pak platí x x 0 a λx = Bx Z poslední rovnosti vyplývá pomocí přechodu ke komplexně konjugovaným maticím také rovnost λx = x B, a tedy také x x(λ λ) = x (λ λ)x = x Bx x B x = 0, neboť B = B Proto λ = λ Cvičení 111 Dokažte, že každé vlastní číslo kososymetrické matice nebo kosohermitovské matice je ryze imaginární Tvrzení 116 Je-li A čtvercová reálná (komplexní) matice řádu n, P reálná (komplexní) regulární matice stejného řádu a B = P 1 AP, pak obě matice A a B mají stejný charakteristický polynom, a proto rovněž σ(a) = σ(b), tj obě mají také stejné spektrum Důkaz Podle Věty 1015 o součinu determinantů platí pro každý reálné (komplexní) číslo λ det(a λi n ) = det I n det(a λi n ) = det(p 1 P) det(a λi n ) = = det P 1 det(a λi n ) det P = det(p 1 (A λi n )P) = = det(p 1 AP P 1 λi n P) = = det(b λi n ) Důsledek 117 Předpokládáme, že V je vektorový prostor nad reálnými (komplexními) čísly a F : V V je lineární zobrazení Dále předpokládáme, že A a B jsou dvě báze prostoru V Označíme A matici [F ] A lineárního zobrazení F vzhledem k bázi A a B matici [F ] B zobrazení F vzhledem k bázi B Potom jsou charakteristické polynomy obou matic A a B stejné a platí rovnost σ(a) = σ(b)
6 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 6 Důkaz Podle Tvrzení 713 platí [F ] B = P 1 [F ] A P, kde P = [I] BA je matice přechodu od báze A k bázi B Protože matice přechodu [I] BA je regulární, plynou všechna tvrzení bezprostředně z předchozího Tvrzení 116 Tento důsledek ukazuje, že vlastní čísla a spektrum jsou spíše vlastnosti lineárních zobrazení než pouze vlastnosti matic Každá reálná (komplexní) matice A řádu n určuje lineární zobrazení F : R n R n (F : C n C n ) předpisem F (x) = Ax Matice A má vlastní číslo λ právě když existuje nenulový vektor x R n (C n ), pro který platí Ax = λx Pro lineární zobrazení F určené maticí A pak platí F (x) = Ax = λx Tyto úvahy vedou k následující definici Definice 118 Je-li F : V V lineární operátor na reálném (komplexním) vektorovém prostoru V, pak skalár λ nazýváme vlastní číslo lineárního operátoru A pokud existuje nenulový vektor x U, pro který platí F (x) = λx Je-li λ vlastní číslo operátoru F, pak každý vektor x V, pro který platí F (x) = λx, nazýváme vlastní vektor lineárního operátoru F příslušný vlastnímu číslu λ Množinu všech vlastních čísel operátoru F označujeme σ(f ) a nazýváme spektrum operátoru F Bezprostřením důsledkem Tvrzení 114 je následující tvrzení Tvrzení 119 Je-li F : U U lineární operátor na komplexním vektorovém prostoru U, pak existuje vlastní číslo λ operátoru F Pokusíme se vyjasnit, do jaké míry lze matici lineárního operátoru F : V V zjednodušit vhodnou volbou báze B prostoru V Definice 1110 Lineární operátor F : V V na reálném (komplexním) vektorovém prostoru V se nazývá diagonalizovatelný, pokud existuje báze B prostoru V, pro kterou platí, že matice [F ] B operátoru F vzhledem k bázi B je diagonální Reálná (komplexní) matice A řádu n se nazývá diagonalizovatelná, pokud existuje regulární reálná (komplexní) matice P řádu n, pro kterou platí, že součin P 1 AP je diagonální matice Platí tedy, že lineární operátor F : V V je diagonalizovatelný právě když je diagonalizovatelná matice [F ] A tohoto operátoru vzhledem k libovolné bázi A prostoru V Ne každá matice je ale diagonalizovatelná
7 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 7 Úloha 111 Dokažte, že matice není diagonalizovatelná A = ( Řešení Pro matici A platí A 2 = 0 Pokud by byla diagonalizovatelná, existovaly by regulární matice P a diagonální matice D takové, že P 1 AP = D Potom by platilo D 2 = P 1 APP 1 AP = P 1 A 2 P = 0, proto rovněž D = 0, a tedy A = PDP 1 = 0, což je spor Matice A proto není diagonalizovatelná Následující tvrzení udává nutnou a postačující podmínku pro diagonalizovatelnost Tvrzení 1111 Lineární operátor F : V V na reálném (komplexním) vektorovém prostoru V je diagonalizovatelný právě když existuje báze prostoru V složená z vlastních vektorů operátoru F Čtvercová (komplexní) matice A řádu n je diagonalizovatelná právě když existuje báze prostoru R n (C n ), která je složená z vlastních vektorů matice A Důkaz Nejdříve dokážeme druhou část týkající se matic Pokud je matice A diagonalizovatelná, existuje regulární matice P a diagonální matice D, pro které platí P 1 AP = D, neboli AP = PD Označme λ λ 2 0 D = 0 0 λ n ) Potom platí A[P 1 P 2 P n ] = [P 1 P 2 P n ] λ λ λ n
8 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 8 Pro každé k = 1, 2,, n tak platí AP k = λ k P k Každý sloupcový vektor P k je tak vlastním vektorem matice A příslušným vlastnímu číslu λ k Matice P je regulární, její sloupcové vektory jsou proto lineárně nezávislé a tvoří tak bázi prostoru R n (C n ) Pokud naopak existuje báze u 1,, u n prostoru R n (C n ) složená ze samých vlastních vektorů matice A, platí pro každé k = 1, 2,, n, že Au k = λ k u k pro nějaké skaláry λ k Označíme P = [u 1 u 2 u n ], tato matice je regulární, protože sloupce jsou lineárně nezávislé Dále označíme λ λ 2 0 D = 0 0 λ n Stejně jako v předchozí části důkazu ukážeme, že potom AP = PD, neboli P 1 AP = D, matice A je proto diagonalizovatelná Nyní dokážeme první část tvrzení Zvolíme bázi A : v 1, v 2,, v n prostoru V libovolně Označíme A = [F ] A matici lineárního operátoru F vzhledem k bázi A Podle předchozí části důkazu existuje reálná (komplexní) regulární matice P = (c ij ) řádu n taková, že P 1 AP = D pro nějakou diagonální matici D Označíme n u j = c ij v i i=1 pro i = 1, 2,, n Protože je matice P regulární, je posloupnost vektorů B : u 1,, u n lineárně nezávislá a tedy báze prostoru V Matice P se potom rovná matici [I] BA identického zobrazení vzhledem k bázím B a A a je tedy maticí přechodu od báze A k bázi B Matice [F ] B lineárního zobrazení F : V V vzhledem k bázi B se potom rovná podle Tvrzení 713 rovná matici [I] AB [F ] A [I] BA = P 1 AP = D V první části posledního důkazu jsme dokázali rovněž následující jednoduchý důsledek Důsledek 1112 Je-li A čtvercová matice řádu n a P regulární matice taková, že P 1 AP = D, kde D je digonální matice, pak na hlavní diagonále matice D jsou všechna vlastní čísla matice A Následující tvrzení ukazuje postačující podmínku, kdy jsou nějaká matice nebo lineární operátor diagonalizovatelné
9 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 9 Tvrzení 1113 Jsou-li λ 1,, λ m navzájem různá vlastní čísla matice A řádu n a u i 0 je vlastní vektor matice A příslušný vlastnímu číslu λ i pro libovolné i = 1,, m, pak je posloupnost vektorů u 1,, u m lineárně nezávislá Má-li matice A řádu n celkem n navzájem různých vlastních čísel, pak je diagonalizovatelná Má-li lineární operátor F : V V celkem n navzájem různých vlastních čísel, pak je diagonalizovatelný Důkaz K důkazu první části stačí dokázat, že pro každé k = 1,, m, jsou vektory u 1,, u k lineárně nezávislé Toto tvrzení zřejmě platí pro k = 1, protože vektor u 1 0 Pokud je k = 2,, m, tak budeme předpokládat, že posloupnost u 1,, u k 1 je lineárně nezávislá a dokážeme, že také posloupnost u 1,, u k je lineárně nezávislá Nechť tedy platí a 1 u 1 + a 2 u a k u k = 0 pro nějaké skaláry a 1,, a k Potom také A(a 1 u 1 + a 2 u a k u k ) = a 1 λ 1 u 1 + a 2 λ 2 u a k λ k u k = 0 Rovněž platí λ k a 1 u 1 + λ k a 2 u λ k a k u k = 0 Odečtením posledních dvou rovností dostaneme tj (λ 1 λ k )a 1 u 1 + (λ 2 λ k )a 2 u (λ k λ k )a k u k = 0, (λ 1 λ k )a 1 u 1 + (λ 2 λ k )a 2 u (λ k 1 λ k )a k 1 u k 1 = 0 Z lineární nezávislosti vektorů u 1,, u k 1 a vzájemné různosti skalárů λ 1,, λ k plyne a 1 = a 2 = = a k 1 = 0, a proto musí platit a k u k = 0 Protože u k 0, dostáváme také a k = 0 Pokud má matice A celkem n navzájem různých vlastních čísel a jsou-li u i 0 vlastní vektory příslušné vlastním číslům λ i pro i = 1, 2,, n, pak je posloupnost vektorů u 1,, u n lineárně nezávislá podle první části důkazu a tedy bází prostoru R n (C n ) Matice A je proto diagonalizovatelná podle Tvrzení 1111
10 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 10 Tvrzení 1114 Čtvercová reálná (komplexní) matice A řádu n je diagonalizovatelná právě když pro každé vlastní číslo λ matice A platí, že algebraická násobnost λ se rovná dimenzi nulového prostoru matice A λi n, tj číslu dim N (A λi n ) Důkaz Je-li matice A diagonalizovatelná, existuje regulární matice P, pro kterou platí P 1 AP = D, kde D je diagonální matice Na hlavní diagonále matice D jsou vlastní čísla λ 1, λ 2,, λ n matice A podle Důsledku 1112 Budeme předpokládat, že přesně k z těchto vlastních čísel se rovná nějakému reálnému (komplexnímu) číslu λ, tj že algebraická násobnost vlastního čísla λ se rovná k Diagonální matice D λi n má potom právě k nul na hlavní diagonále, její hodnost je proto n k Protože A λi n = P(D λi n )P 1, má matice A λi n také hodnost n k Její nulový prostor má proto dimenzi k K důkazu obrácené implikace budeme předpokládat, že λ 1,, λ t jsou všechna navzájem různá vlastní čísla matice A Algebraickou násobnost vlastního čísla λ i označíme m i pro i = 1,, t Podle Základní věty algebry 113 platí m 1 + m m t = n a podle předpokladu o matici A dostáváme m i = dim N (A λ i I n ) pro i = 1, 2,, t V každém z podprsotorů N (A λ i I n ) zvolíme bázi Dokážeme, že posloupnost vektorů x i1, x i2,, x imi x 11, x 12,, x 1m1, x 21, x 22,, x 2m2,, x t1, x t2,, x tmt je lineárně nezávislá Pokud pro nějaké skaláry a ij, označíme m i a ij x ij = 0 i=1 j=1 m i y i = a ij x ij j=1
11 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 11 pro i = 1,, t Potom y i N (A λ i I n ), tj y i je vlastní vektor matice A odpovídající vlastnímu číslu λ i, pro každé i = 1,, t Kromě toho y 1 + y y t = 0 Pokud by byl některý z vektorů y i 0, označili bychom symbolem J množinu {i = 1, 2,, t : y i 0} = Z poslední rovnosti bychom pak dostali y i = 0, i J tj vektory y i pro i J by byly lineárně závislé Protože jsou to vlastní vektory odpovídající různým vlastním číslům matice A, dostali bychom spor s Tvrzením 1113 Proto y i = 0 pro každé i = 1, 2,, t Protože m i 0 = y i = a ij x ij a vektory x i1,, x imi tvoří bázi podprostoru N (A λ i I n ), platí a i1 = a i2 = = a imi = 0 pro každé i = 1,, t Posloupnost vektorů j=1 x 11, x 12,, x 1m1, x 21, x 22,, x 2m2,, x t1, x t2,, x tmt je proto skutečně lineárně nezávislá, a protože obsahuje n prvků, tvoří bázi prostoru R n 1 (C n 1 ) Prostor R n 1 (C n 1 ) tak má bázi složenou z vlastních vektorů matice A, matice A je proto diagonalizovatelná podle Tvrzení 1111 Následující věta je často nazývána spektrální věta pro diagonalizovatelné matice Věta 1115 Čtvercová matice A řádu n se spektrem σ(a) = {λ 1,, λ t } je diagonalizovatelná právě když existují matice E 1,, E t řádu n, pro které platí 1 A = λ 1 E 1 + λ 2 E λ t E t, 2 E 2 i = E i pro každé i = 1, 2,, t, 3 E i E j = 0 pro libovolné dva různé indexy i, j = 1, 2,, t, 4 E 1 + E E t = I n Dále pro diagonalizovatelnou matici A platí, že
12 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 12 5 matice E i jsou jednoznačně určené maticí A a vlastnostmi 1, 2, 3, 4, 6 hodnost každé z matic E i se rovná algebraické násobnosti charkteristického čísla λ i, 7 je-li f(x) = c 0 + c 1 x + c k x k libovolný polynom s komplexními koeficienty, pak platí f(a) = c 0 I n + c 1 A + + c k A k = f(λ 1 )E 1 + f(λ 2 )E f(λ k )E k, 8 nějaká matice B komutuje s maticí A právě tehdy, když komutuje s každou z matic E i pro i = 1, 2,, t Důkaz Označíme m i algebraickou násobnost vlastního čísla λ i pro i = 1, 2,, t Z diagonalizovatelnosti matice A pak vyplývá existence regulární matice P řádu n, pro kterou platí λ 1 I m1 0 0 P 1 0 λ 2 I m2 0 AP = 0 0 λ t I mt Označíme pro i = 1, 2,, t symbolem D i matici, kterou dostaneme z blokové matice na pravé straně poslední rovnosti tak, že nahradíme všechny výskyty vlastního čísla λ i číslem 1 a výskyty ostatních vlastních čísel λ j pro j i číslem 0 Například I m2 0 D 2 = Potom platí I n = D 1 + D D t, P 1 AP = λ 1 D 1 + λ 2 D λ t D t, A = λ 1 PD 1 P 1 + λ 2 PD 2 P λ t PD t P 1 Položíme E i = PD i P 1 pro i = 1, 2,, t a dostaneme tak ze třetí rovnosti vlastnost 1 Protože D 2 i = D i a D i D j = 0 pro libovolné různé
13 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 13 indexy i, j = 1, 2,, t, dostáváme E 2 i = PD i P 1 PD i P 1 = PD i P 1 = E i, E i E j = PD i P 1 PD j P 1 = PD i D j P 1 = 0, E E t = P(D D t )P 1 = PI n P 1 = I n, což dokazuje vlastnosti 2, 3, 4 Abychom dokázali opačnou implikaci, budeme předpokládat, že pro matici A existují matice E 1,, E t splňující podmínky 1, 2, 3, 4 Jako první krok dokážeme, že platí S(E E j ) = S(E 1 ) + + S(E j ) pro každé j = 1,, t Je-li x S(E E j ), existuje vektor y C n 1 takový, že x = (E 1 + E E j )y = E 1 y + + E j y Jelikož E i y S(E i ) pro každé i = 1,, j, platí x = E 1 y + + E j y S(E 1 ) + + S(E j ), proto S(E E j ) S(E 1 ) + + S(E j ) K důkazu opačné inkluze předpokládejme, že x S(E 1 ) + + S(E j ) Existují tedy vektory x i S(E i ) pro i = 1,, j takové, že x = x 1 + +x j Z x i S(E i ) plyne existence vektoru y i C n 1, pro který platí x i = E i y i Potom platí j j j j j j j ( E i )x = ( E i )( x i ) = E i x k = E i E k y k = i=1 i=1 k=1 i=1 k=1 i=1 k=1 j j = E i y i = x i = x i=1 i=1 Tím je dokázána opačná inkluze S(E E j ) S(E 1 ) + + S(E j ) Dále dokážeme, že pro každé j = 1, t 1 platí S(E E j ) S(E j+1 ) = {0}
14 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 14 Pokud x S(E E j ) S(E j+1 ), existují vektory y, y j+1 C n 1 takové, že x = (E E j )y = E j+1 y j+1 Z této rovnosti a z podmínek 2, 3 dostáváme j x = E j+1 y j+1 = E j+1 E j+1 y j+1 = E j+1 (E 1 + +E j )y = E j+1 E i y = 0, i=1 čímž je rovnost S(E E j ) S(E j+1 ) = {0} dokázána Z této rovnosti, z dříve dokázané rovnosti S(E E t ) = S(E 1 ) + + S(E t ), a opakovaným použitím Tvrzení 622 pak dostaneme n = dim I n = dim S(E E t 1 + E t ) = = dim(s(e 1 ) + + S(E t 1 ) + S(E t )) = = dim(s(e E t 1 ) + S(E t )) = = dim S(E E t 1 ) + dim S(E t ) dim(s(e E j ) S(E j+1 )) = = dim S(E E t 2 + E t 1 ) + dim S(E t ) = = dim S(E 1 ) + + dim S(E t 1 ) + dim S(E t ) Označíme n i = dim S(E i ) pro i = 1,, t V každém z podprostorů S(E i ) zvolíme bázi x i1,, x ini Posloupnost vektorů x 11,, x 1n1, x 21,, x 2n2,, x t1,, x tnt generuje podprostor C n 1, který obsahuje každý z podprostorů S(E i ) pro i = 1, 2,, t, a tedy také jejich součet S(E 1 )+ +S(E t ) = S(E 1 + +E t ) = S(I n ) = C n 1 V posloupnosti je celkem n n t = dim S(E 1 ) + + dim S(E t ) = n prvků, a protože generuje prostor C n 1, který má dimenzi n, musí být rovněž lineárně nezávislá podle Tvrzení 69, a tedy báze prostoru C n 1 Sloupcový prostor matice Q = [x 11 x 1n1 x 21 x 2n2 x t1 x tnt ] má proto dimenzi n a matice Q je tak regulární Protože I n = Q 1 Q, platí podle druhé části Tvrzení 37 e k = I k = Q 1 Q k
15 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 15 pro každé k = 1,, n Připomeňme, že e k označuje k-tý vektor standardní báze prostoru C n 1 Protože x il S(E i ), existuje vektor y il C n 1, pro který platí x il = E i y il Potom platí E i x il = E i E i y il = E i y il = x il, zatímco pro každé j i, j {1, 2,, t}, platí podle podmínky 3 E j x il = E j E i x il = 0x il = 0 Dokážeme nyní, že součin Q 1 AQ je diagonální matice Rovná-li se k-tý sloupcový vektor matice Q vektoru x il, dostáváme s využitím podmínky 1, že (Q 1 AQ) k = Q 1 AQ k = Q 1 ( λ j E j )x il = Q 1 λ j E j x il = j=1 j=1 = Q 1 λ i E i x il = Q 1 λ i x il = λ i Q 1 Q k = λ i e k Pro každé k = 1,, n tak platí, že v k-tém sloupci součinu Q 1 AQ je jediný případně nenulový prvek na hlavní diagonále (a rovná se jednomu z vlastních čísel λ i, i = 1,, t) Matice Q 1 AQ je proto diagonální a matice A je diagonalizovatelná Zbývá dokázat, že pro každou diagonalizovatelnou matici A platí vlastnosti 5, 6, 7, 8 Protože matice D i má hodnost m i, má tutéž hodnost i matice E i = PD i P 1, což dokazuje 6 S použitím vlastností 2, 3, 4 můžeme spočítat A 2 = (λ 1 E 1 + λ 2 E λ t E t )(λ 1 E 1 + λ 2 E λ t E t ) = = λ i E i λ j E j = λ 2 i E 2 i = λ 2 i E i i,j=1 i=1 Jestliže nyní předpokládáme, že pro nějaké l 2, pak dostáváme, že i=1 A l = λ l ie i i=1 A l+1 = (λ 1 E 1 + λ 2 E λ t E t )(λ l 1E 1 + λ l 2E λ l te t ) = = λ i E i λ l je j = λ l+1 i E 2 i = λ l+1 i E i i=1 j=1 i=1 i=1
16 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 16 Protože rovněž A 0 = I n = E E t = λ 0 1E λ 0 t E t, rovnost A l = λ l ie i i=1 platí pro každé nezáporné celé číslo l Pro každé číslo j = 0,, k tak dostáváme c j A j = c j λ j i E i i=1 a tedy k k k f(a) = c j A j = c j ( λ j i E i) = ( c j λ j i )E i = f(λ i )E i j=0 j=0 i=1 i=1 j=0 i=1 Abychom dokázali jednoznačnost matic E 1,, E t splňujících podmínky 1, 2, 3, 4, budeme předpokládat, že A = λ 1 F 1 + λ 2 F λ t F t, kde F F t = I n, F i F i = F i a F i F j = 0 pro libovolné i j, i, j {1, 2,, t} Potom Proto pro i j dostáváme E i A = AE i = λ i E i, F j A = AF j = λ j F j λ j E i F j = E i (AF j ) = (E i A)F j = λ i E i F j, proto (λ i λ j )E i F j = 0, neboli E i F j = 0 Můžeme tak spočítat, že platí E i = E i I n = E i ( F j ) = E i F i = ( E j )F i = I n F i = F i j=1 j=1 pro každé i = 1,, t Tím je dokázána jednoznačnost matic E i, tj podmínka 5 Zbývá dokázat podmínku 8 Z podmínky 1 okamžitě vyplývá, že pokud matice B komutuje se všemi maticemi E i pro i = 1,, t, komutuje rovněž s maticí A Abychom dokázali opačnou implikaci, vyjádříme každou matici E i jako polynom v matici A Označme g(x) = (x λ 1 )(x λ 2 ) (x λ t )
17 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 17 a g i (x) = g(x) x λ i pro i = 1,, t Polynom p i (x) má stupeň t 1 a kořeny λ j pro j i Podle vlastnosti 7 platí g i (A) = g i (λ 1 )E g i (λ t )E t = g i (λ i )E i Označíme-li c i = g i (λ i ) 0, dostaneme že E i = c 1 i g i (A) Pokud tedy matice B komutuje s maticí A, komutuje také s každou maticí g i (A) = E i pro i = 1,, t c 1 i Cvičení 112 Zjistěte pro několik matic A, jsou-li diagonalizovatelné, pokud ano, najděte regulární matici P, pro kterou platí, že P 1 AP je diagonální matice, a najděte spektrální rozklad matice A Unitární podobnost Dále se budeme zabývat otázkou, kdy pro diagonalizovatelnou matici A řádu n existuje ortogonální matice P, pro kterou platí, že P 1 AP je diagonální matice Nebo jinak řečeno, kdy existuje ortonormální báze prostoru C n 1 tvořená vlastními vektory matice A Definice 1116 Říkáme, že komplexní čtvercová matice A řádu n je unitárně diagonalizovatelná, pokud existují unitární matice P a diagonální matice D, pro které platí P 1 AP = D Připomeňme si, že čtvercová matice P je unitární právě když P 1 = P Tvrzení 1117 Je-li komplexní matice A řádu n unitárně diagonalizovatelná, pak platí AA = A A Důkaz Jestliže existují unitární matice P a diagonální matice D, pro které platí P AP = D, pak přechodem ke komplexně konjugovaným maticím dostaneme rovněž P A P = D Protože pro diagonální matici D platí D D = DD, dostáváme postupně P AP P A P = DD = D D = P A P P AP P AA P = P A AP AA = A A
18 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 18 Definice 1118 Komplexní čtvercová matice A se nazývá normální, pokud platí A A = AA Třída normálních matic je velmi široká, jak se můžete přesvědčit v následujícícm cvičení Cvičení 113 Dokažte, že všechny matice následujících typů jsou normální: hermitovské matice, kosohermitovské matice, reálné symetrické matice, reálné kososymetrické matice, unitární matice, ortogonální matice, diagonální matice, všechny matice tvaru P AP, kde A je normální matice a P je unitární matice Lemma 1119 Je-li A normální matice a x vlastní vektor matice A příslušný vlastnímu číslu λ, pak je x také vlastní vektor matice A příslušný vlastnímu číslu λ Důkaz Především si všimněme, že je-li A normální matice, pak pro každé komplexní číslo λ platí (A λi n ) (A λi n ) = (A λi n)(a λi n ) = = A A λa λa + λλi n = = AA λa λa + λλi n = = (A λi n )(A λi n ) Matice A λi n je proto také normální Je-li nyní x 0 vlastní vektor matice A odpovídající vlastnímu číslu λ, pak označíme B = A λi n Platí tedy B B = BB a Bx = 0 Označíme dále y = B x Potom platí 0 = (Bx) (Bx) = x B Bx = x BB x = y y Odtud plyne, že y = 0, tj 0 = B x = (A λi n )x, tj A x = λx Vektor x je tak vlastní číslem matice A odpovídajícím vlastnímu číslu λ této matice Tvrzení 1120 Je-li A normální matice, pak pak vlastní vektory odpovídající různým vlastním číslům matice A jsou ortogonální Důkaz Předpokládejme nyní, že λ 1, λ 2 jsou dvě různá vlastní čísla matice A a x 1, x 2 jsou jim odpovídající vlastní vektory Právě jsme dokázali, že pak rovněž A x 1 = λ 1 x 1 Spočítáme dále, že λ 1 x 1x 2 = (λ 1 x 1 ) x 2 = (A x 1 ) x 2 = (x 1A)x 2 = x 1(Ax 2 ) = λ 2 x 1x 2
19 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 19 Protože λ 1 λ 2, plyne odtud x 1 x 2 = 0, tj vektory x 1 a x 2 jsou ortogonální Věta 1121 Komplexní matice A řádu n je unitárně diagonalizovatelná právě když je normální Důkaz Každá unitárně diagonalizovatelná matice A je normální podle Tvrzení 1117 Je-li naopak matice A normální, pak každý vlastní vektor x matice A je současně vlastním vektorem matice A Zvolíme tedy vlastní vektor x 1 jednotkové délky matice A příslušný vlastnímu číslu λ σ(a) Podle Lemma 1119 je x 1 rovněž vlastní vektor matice A příslušný vlastnímu číslu λ Označíme U 1 = L(x 1 ) = {y C n 1 : y x 1 = 0}, ortogonální doplněk vektoru x 1 v prostoru C n 1 Dokážeme, že pro každý vektor y U 1 platí, že také Ay U 1 Skutečně, (Ay) x 1 = (y A )x 1 = y (A x 1 ) = y λx 1 = 0 Podobně dokážeme, že také A y U 1 Lineární zobrazení F (y) = Ay je tedy lineární operátor na prostoru U 1 Podle Tvrzení 119 existuje (jednotkový) vlastní vektor x 2 lineárního operátoru F, tj λ 2 x 2 = F (x 2 ) = Ax 2 Vektor x 2 je tak vlastním vektorem matice A a tedy i matice A Označíme U 2 = L(x 1, x 2 ) Stejně jako v případě prostoru U 1 dokážeme, že pro každý vektor y U 2 platí jak Ay U 2 tak i A y U 2 Prostor U 2 je tak invariantním podprostorem operátoru F, existuje tedy jednotkový vlastní vektor x 3 U 2 operátoru F odpovídající vlastnímu číslu λ 3, atd Takto postupně sestrojíme ortonormální posloupnost x 1, x 2,, x n tvořenou vlastními vektory matice A Pro unitární matici P = [x 1 x 2 x n ] pak platí AP = PD, kde D je diagonální matice obsahující na hlavní diagonále postupně vlastní čísla λ 1, λ 2,, λ n Matice A je proto unitárně diagonalizovatelná Důsledek 1122 Je-li A normální matice a A = λ 1 E 1 + λ 2 E λ t E t spektrální rozklad matice A podle Věty 1115, pak všechny matice E i jsou
20 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 20 hermitovské pro i = 1,, t Obráceně, je-li A diagonalizovatelná komplexní matice a všechny matice E i ve spektrálním rozkladu A = λ 1 E λ t E t jsou hermitovské, pak je matice A normální Důkaz Je-li A normální, pak A = PDP 1 pro nějakou unitární matici P a diagonální matici D podle Věty 1121, pak matice E i = PD i P 1 = PDP sestrojené v důkazu Věty 1115 jsou hermitovské Obráceně, jsou-li všechny matice E i ve spektrálním rozkladu A = λ 1 E λ t E t hermitovské, pak rovněž je spektrální rozklad matice A Pak což dokazuje, že A je normální A = λ 1 E λ 1 λ t E t AA = λ 1 λ 1 E λ t λ t E t = A A, Závěrem části o vlastních číslech a vlastních vektorech si ještě ukážeme, jak lze zesílit Větu 925 o URV-faktorizaci Tvrzení 1123 Je-li A C m n (R m n ) komplexní (reálná) matice, pak každé vlastní číslo matice A A (A T A) je nezáporné reálné číslo Důkaz Je-li A komplexní matice, pak součin A A je hermitovská matice řádu n Je-li to reálná matice, pak součin A T A je symetrická matice řádu n V obou případech jsou všechna vlastní čísla matice A A (A T A) reálná podle Tvrzení 115 Je-li λ nějaké vlastní číslo matice A A a x 0 vlastní vektor odpovídající λ, pak platí A Ax = λx Vynásobíme tuto rovnost zleva vektorem x a dostaneme Ax 2 = x A Ax = λx x = λ x 2, odkud vyplývá λ = Ax 2 x 2 0 V případě reálné matice A platí A = A T, proto rovněž λ 0 pro každé vlastní číslo λ matice A T A Dále si ještě ukážeme následující tvrzení Tvrzení 1124 Pro každou reálnou (komplexní) matici A tvaru m n platí r(a T A) = r(a) = r(aa T ), (r(a A) = r(a) = r(aa )),
21 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 21 S(A T A) = S(A T ), (S(A A) = S(A )), S(AA T ) = S(A), (S(AA ) = S(A)), N (A T A) = N (A), (N (A A) = N (A)), N (AA T ) = N (A T ), (N (AA ) = N (A )) Důkaz Dokážeme pouze reálnou část tvrzení, komplexní část se dokáže analogicky, pouze všude nahradíme transponovanou matici A T maticí A Nejdříve dokážeme, že N (A T ) S(A) = {0} Je-li x N (A T ) S(A), pak platí A T x = 0 a současně x = Ay pro nějaký vektor y R n 1 Odtud plyne x T x = y T A T x = 0 a proto x = 0 Z Tvrzení 619 pak plyne r(a T A) = r(a) dim N (A T S(A)) = r(a) Zaměníme-li role A T a A, dostaneme rovněž r(aa T ) = r(a T ) = r(a) K důkazu druhé části tvrzení si napřed všimněme, že S(A T A) S(A T ) Protože dále dim S(A T A) = r(a T A) = r(a) = r(a T ) = dim S(A T ), vyplývá odtud rovnost S(A T A) = S(A T ) Třetí část tvrzení ihned vyplývá z druhé, zaměníme-li role A a A T K důkazu čtvrté části opět stačí uvědomit si, že N (A) N (A T A), a dále dim N (A) = n r(a) = n r(a T A) = dim N (A T A) Proto N (A) = N (A T A) Poslední část tvrzení opět ihned vyplývá z předchozí, pokud zaměníme role A a A T Nyní můžeme dokázat slíbené zesílení Věty 925 Věta 1125 Předpokládáme, že A je reálná (komplexní) matice tvaru m n a hodnosti r Potom existují reálná diagonální matice D r r řádu r a ortogonální (unitární) matice U řádu n a V řádu m takové, že platí A = U ( Dr r ) V T, (A = U ( Dr r ) V ) Důkaz Dokážeme pouze část týkající se komplexních matic Pro reálné matice se věta dokáže analogicky
22 KAPITOLA 11 VLASTNÍ ČÍSLA A VLASTNÍ VEKTORY 22 Matice A A je normální, neboť (A A) A A = A AA A = A A(A A) Podle Věty 1121 je matice A A unitárně diagonalizovatelná, existuje tedy podle Věty 1121 unitární matice V řádu n taková, že V A AV = D, kde D je diagonální matice s nezápornými reálnými čísly λ i (vlastní čísla matice A A) na hlavní diagonále Protože r(a A) = r(a) = r, můžeme předpokládat, že λ i > 0 pro i = 1,, r a λ i = 0 pro i = r + 1,, n Označíme σ i = λ i pro i = 1,, n a u i = Av i σ i pro i = 1,, k Potom platí pro každé dva indexy i, j {1, 2,, r} u ju i = v j A σ i Av i σ i = v j A Av i λ i = λ iv j v i λ i = v j v i = δ ij Posloupnost vektorů u 1,, u k je tak ortonormální, protože ortonormální je posloupnost vektorů v 1,, v n Můžeme ji proto doplnit do ortonormální báze u 1,, u k, u k+1,, u n prostoru C n 1 Označíme U = [u 1 u n ] Potom pro i-tý sloupec součinu U AV platí [U AV] i = U Av i = U σ i u i Prvek na místě (j, i) v součinu U AV se proto rovná [U AV] ji = [U ] j σu i = u jσ i u i = σ i δ ji Součin U AV je proto diagonální matice D, prvky na hlavní diagonále D se rovnají σ i = λ i, kde λ i jsou vlastní čísla součinu A A Odtud hned dostaneme (protože matice U a V jsou unitární), že A = UDV Číslům σ i > 0 se říká singulární hodnoty matice A Jsou určené jednoznačně maticí A, neboť z rovnosti A = UDV plyne V A AV = V A UU AV = D D = D 2 Druhé mocniny singulárních hodnot σi 2 jsou proto vlastní hodnoty součinu A A Geometrický význam singulárních hodnot si ukážeme v kapitole o kvadratických formách
Učební texty k státní bakalářské zkoušce Matematika Vlastní čísla a vlastní hodnoty. študenti MFF 15. augusta 2008
 Učební texty k státní bakalářské zkoušce Matematika Vlastní čísla a vlastní hodnoty študenti MFF 15. augusta 2008 1 14 Vlastní čísla a vlastní hodnoty Požadavky Vlastní čísla a vlastní hodnoty lineárního
Učební texty k státní bakalářské zkoušce Matematika Vlastní čísla a vlastní hodnoty študenti MFF 15. augusta 2008 1 14 Vlastní čísla a vlastní hodnoty Požadavky Vlastní čísla a vlastní hodnoty lineárního
Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru. Kvadratická forma v n proměnných je tak polynom n proměnných s
 Kapitola 13 Kvadratické formy Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru f(x 1,..., x n ) = a ij x i x j, kde koeficienty a ij T. j=i Kvadratická forma v n proměnných
Kapitola 13 Kvadratické formy Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru f(x 1,..., x n ) = a ij x i x j, kde koeficienty a ij T. j=i Kvadratická forma v n proměnných
Vlastní číslo, vektor
 [1] Vlastní číslo, vektor motivace: směr přímky, kterou lin. transformace nezmění invariantní podprostory charakteristický polynom báze, vzhledem ke které je matice transformace nejjednodušší podobnost
[1] Vlastní číslo, vektor motivace: směr přímky, kterou lin. transformace nezmění invariantní podprostory charakteristický polynom báze, vzhledem ke které je matice transformace nejjednodušší podobnost
[1] Motivace. p = {t u ; t R}, A(p) = {A(t u ); t R} = {t A( u ); t R}
![[1] Motivace. p = {t u ; t R}, A(p) = {A(t u ); t R} = {t A( u ); t R} [1] Motivace. p = {t u ; t R}, A(p) = {A(t u ); t R} = {t A( u ); t R}](/thumbs/26/7692117.jpg) Vlastní číslo, vektor motivace: směr přímky, kterou lin. transformace nezmění invariantní podprostory charakteristický polynom báze, vzhledem ke které je matice transformace nejjednodušší podobnost s diagonální
Vlastní číslo, vektor motivace: směr přímky, kterou lin. transformace nezmění invariantní podprostory charakteristický polynom báze, vzhledem ke které je matice transformace nejjednodušší podobnost s diagonální
Lineární algebra : Vlastní čísla, vektory a diagonalizace
 Lineární algebra : Vlastní čísla, vektory a diagonalizace (14. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 21. dubna 2014, 19:37 1 2 14.1 Vlastní čísla a vlastní vektory Nechť je
Lineární algebra : Vlastní čísla, vektory a diagonalizace (14. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 21. dubna 2014, 19:37 1 2 14.1 Vlastní čísla a vlastní vektory Nechť je
1 Linearní prostory nad komplexními čísly
 1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti
 Kapitola 5 Vektorové prostory V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti operací sčítání a násobení
Kapitola 5 Vektorové prostory V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti operací sčítání a násobení
Vlastní čísla a vlastní vektory
 Kapitola 15 Vlastní čísla a vlastní vektory V této a následujících kapitolách budeme zkoumat jeden z nejdůležitějších pojmů tohoto kurzu. Definice15.1 Buď A:V Vlineárnízobrazení,Vvektorovýprostornad tělesem
Kapitola 15 Vlastní čísla a vlastní vektory V této a následujících kapitolách budeme zkoumat jeden z nejdůležitějších pojmů tohoto kurzu. Definice15.1 Buď A:V Vlineárnízobrazení,Vvektorovýprostornad tělesem
MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij]
![MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij]](/thumbs/58/41721403.jpg) MATICE Matice typu m/n nad tělesem T je soubor m n prvků z tělesa T uspořádaných do m řádků a n sloupců: a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] a m1 a m2 a mn Prvek a i,j je prvek matice A na místě
MATICE Matice typu m/n nad tělesem T je soubor m n prvků z tělesa T uspořádaných do m řádků a n sloupců: a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] a m1 a m2 a mn Prvek a i,j je prvek matice A na místě
Definice : Definice :
 KAPITOLA 7: Spektrální analýza operátorů a matic [PAN16-K7-1] Definice : Necht H je komplexní Hilbertův prostor. Řekneme, že operátor T B(H) je normální, jestliže T T = T T. Operátor T B(H) je normální
KAPITOLA 7: Spektrální analýza operátorů a matic [PAN16-K7-1] Definice : Necht H je komplexní Hilbertův prostor. Řekneme, že operátor T B(H) je normální, jestliže T T = T T. Operátor T B(H) je normální
(2) [B] Nechť G je konečná grupa tvořena celočíselnými maticemi roměru 2 2 s operací násobení. Nalezněte všechny takové grupy až na izomorfizmus.
![(2) [B] Nechť G je konečná grupa tvořena celočíselnými maticemi roměru 2 2 s operací násobení. Nalezněte všechny takové grupy až na izomorfizmus. (2) [B] Nechť G je konečná grupa tvořena celočíselnými maticemi roměru 2 2 s operací násobení. Nalezněte všechny takové grupy až na izomorfizmus.](/thumbs/93/112057876.jpg) (1 [B] Nechť A : R 6 R 6 je lineární zobrazební takové, že A 26 = I. Najděte lineární prostory V 1, V 2 a V 3 takové, že R 6 = V 1 V 2 V 3 dim V 1 = dim V 2 = dim V 3 AV 1 V 1, AV 2 V 2 a AV 3 V 3 (2 [B]
(1 [B] Nechť A : R 6 R 6 je lineární zobrazební takové, že A 26 = I. Najděte lineární prostory V 1, V 2 a V 3 takové, že R 6 = V 1 V 2 V 3 dim V 1 = dim V 2 = dim V 3 AV 1 V 1, AV 2 V 2 a AV 3 V 3 (2 [B]
Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague
 Tomáš Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague 1 / 63 1 2 3 4 5 6 7 8 9 10 11 2 / 63 Aritmetický vektor Definition 1 Aritmetický vektor x je uspořádaná
Tomáš Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague 1 / 63 1 2 3 4 5 6 7 8 9 10 11 2 / 63 Aritmetický vektor Definition 1 Aritmetický vektor x je uspořádaná
15 Maticový a vektorový počet II
 M. Rokyta, MFF UK: Aplikovaná matematika III kap. 15: Maticový a vektorový počet II 1 15 Maticový a vektorový počet II 15.1 Úvod Opakování z 1. ročníku (z kapitoly 8) Označení. Množinu všech reálných resp.
M. Rokyta, MFF UK: Aplikovaná matematika III kap. 15: Maticový a vektorový počet II 1 15 Maticový a vektorový počet II 15.1 Úvod Opakování z 1. ročníku (z kapitoly 8) Označení. Množinu všech reálných resp.
Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice
 Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice Vektorové podprostory K množina reálných nebo komplexních čísel, U vektorový prostor nad K. Lineární kombinace vektorů u 1, u 2,...,u
Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice Vektorové podprostory K množina reálných nebo komplexních čísel, U vektorový prostor nad K. Lineární kombinace vektorů u 1, u 2,...,u
Základy maticového počtu Matice, determinant, definitnost
 Základy maticového počtu Matice, determinant, definitnost Petr Liška Masarykova univerzita 18.9.2014 Matice a vektory Matice Matice typu m n je pravoúhlé (nebo obdélníkové) schéma, které má m řádků a n
Základy maticového počtu Matice, determinant, definitnost Petr Liška Masarykova univerzita 18.9.2014 Matice a vektory Matice Matice typu m n je pravoúhlé (nebo obdélníkové) schéma, které má m řádků a n
z = a bi. z + v = (a + bi) + (c + di) = (a + c) + (b + d)i. z v = (a + bi) (c + di) = (a c) + (b d)i. z v = (a + bi) (c + di) = (ac bd) + (bc + ad)i.
 KOMLEXNÍ ČÍSLA C = {a + bi; a, b R}, kde i 2 = 1 Číslo komplexně sdružené k z = a + bi je číslo z = a bi. Operace s komplexními čísly: z = a + bi, kde a, b R v = c + di, kde c, d R Sčítání Odčítání Násobení
KOMLEXNÍ ČÍSLA C = {a + bi; a, b R}, kde i 2 = 1 Číslo komplexně sdružené k z = a + bi je číslo z = a bi. Operace s komplexními čísly: z = a + bi, kde a, b R v = c + di, kde c, d R Sčítání Odčítání Násobení
Skalární součin je nástroj, jak měřit velikost vektorů a úhly mezi vektory v reálných a komplexních vektorových prostorech.
 Kapitola 9 Skalární součin Skalární součin je nástroj, jak měřit velikost vektorů a úhly mezi vektory v reálných a komplexních vektorových prostorech. Definice 9.1 Je-li x = (x 1,..., x n ) T R n 1 reálný
Kapitola 9 Skalární součin Skalární součin je nástroj, jak měřit velikost vektorů a úhly mezi vektory v reálných a komplexních vektorových prostorech. Definice 9.1 Je-li x = (x 1,..., x n ) T R n 1 reálný
1. Jordanův kanonický tvar
 . Jordanův kanonický tvar Obecně nelze pro zadaný lineární operátor ϕ : U U najít bázi α takovou, že (ϕ) α,α by byla diagonální. Obecně však platí, že pro každý lineární operátor ϕ : U U nad komplexními
. Jordanův kanonický tvar Obecně nelze pro zadaný lineární operátor ϕ : U U najít bázi α takovou, že (ϕ) α,α by byla diagonální. Obecně však platí, že pro každý lineární operátor ϕ : U U nad komplexními
Podobnost matic. Definice 8.6. Dány matice A, B M n (C). Jestliže existuje regulární matice P M n (C) tak,
 Podobnost matic Definice 84 Dány matice A, B M n (C) Jestliže existuje regulární matice P M n (C) tak, že B = P 1 AP, pak říkáme, že matice B je podobná matici A a píšeme A B Takto zavedená binární relace
Podobnost matic Definice 84 Dány matice A, B M n (C) Jestliže existuje regulární matice P M n (C) tak, že B = P 1 AP, pak říkáme, že matice B je podobná matici A a píšeme A B Takto zavedená binární relace
Maticí typu (m, n), kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru:
 3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
Úlohy k přednášce NMAG 101 a 120: Lineární algebra a geometrie 1 a 2,
 Úlohy k přednášce NMAG a : Lineární algebra a geometrie a Verze ze dne. května Toto je seznam přímočarých příkladů k přednášce. Úlohy z tohoto seznamu je nezbytně nutné umět řešit. Podobné typy úloh se
Úlohy k přednášce NMAG a : Lineární algebra a geometrie a Verze ze dne. května Toto je seznam přímočarých příkladů k přednášce. Úlohy z tohoto seznamu je nezbytně nutné umět řešit. Podobné typy úloh se
2. Schurova věta. Petr Tichý. 3. října 2012
 2. Schurova věta Petr Tichý 3. října 2012 1 Podobnostní transformace a výpočet vlastních čísel Obecný princip: Úloha: Řešíme-li matematickou úlohu, je často velmi vhodné hledat její ekvivalentní formulaci
2. Schurova věta Petr Tichý 3. října 2012 1 Podobnostní transformace a výpočet vlastních čísel Obecný princip: Úloha: Řešíme-li matematickou úlohu, je často velmi vhodné hledat její ekvivalentní formulaci
DEFINICE Z LINEÁRNÍ ALGEBRY
 DEFINICE Z LINEÁRNÍ ALGEBRY Skripta Matematické metody pro statistiku a operační výzkum (Nešetřilová, H., Šařecová, P., 2009). 1. definice Vektorovým prostorem rozumíme neprázdnou množinu prvků V, na které
DEFINICE Z LINEÁRNÍ ALGEBRY Skripta Matematické metody pro statistiku a operační výzkum (Nešetřilová, H., Šařecová, P., 2009). 1. definice Vektorovým prostorem rozumíme neprázdnou množinu prvků V, na které
Vlastní čísla a vlastní vektory
 5 Vlastní čísla a vlastní vektor Poznámka: Je-li A : V V lineární zobrazení z prostoru V do prostoru V někd se takové zobrazení nazývá lineárním operátorem, pak je přirozeným požadavkem najít takovou bázi
5 Vlastní čísla a vlastní vektor Poznámka: Je-li A : V V lineární zobrazení z prostoru V do prostoru V někd se takové zobrazení nazývá lineárním operátorem, pak je přirozeným požadavkem najít takovou bázi
2.6. VLASTNÍ ČÍSLA A VEKTORY MATIC
 .6. VLASTNÍ ČÍSLA A VEKTORY MATIC V této kapitole se dozvíte: jak jsou definována vlastní (charakteristická) čísla a vektory čtvercové matice; co je to charakteristická matice a charakteristický polynom
.6. VLASTNÍ ČÍSLA A VEKTORY MATIC V této kapitole se dozvíte: jak jsou definována vlastní (charakteristická) čísla a vektory čtvercové matice; co je to charakteristická matice a charakteristický polynom
PROSTORY SE SKALÁRNÍM SOUČINEM. Definice Nechť L je lineární vektorový prostor nad R. Zobrazení L L R splňující vlastnosti
 PROSTORY SE SKALÁRNÍM SOUČINEM Definice Nechť L je lineární vektorový prostor nad R. Zobrazení L L R splňující vlastnosti 1. (x, x) 0 x L, (x, x) = 0 x = 0, 2. (x, y) = (y, x) x, y L, 3. (λx, y) = λ(x,
PROSTORY SE SKALÁRNÍM SOUČINEM Definice Nechť L je lineární vektorový prostor nad R. Zobrazení L L R splňující vlastnosti 1. (x, x) 0 x L, (x, x) = 0 x = 0, 2. (x, y) = (y, x) x, y L, 3. (λx, y) = λ(x,
Lineární (ne)závislost
 Kapitola 6 Lineární (ne)závislost Také tuto kapitolu zahájíme základní definicí. Definice 6.1 Předpokládáme, že V je vektorový prostor nad tělesem T. Říkáme, že posloupnost vektorů x 1, x 2,..., x n prostoru
Kapitola 6 Lineární (ne)závislost Také tuto kapitolu zahájíme základní definicí. Definice 6.1 Předpokládáme, že V je vektorový prostor nad tělesem T. Říkáme, že posloupnost vektorů x 1, x 2,..., x n prostoru
8 Matice a determinanty
 M Rokyta, MFF UK: Aplikovaná matematika II kap 8: Matice a determinanty 1 8 Matice a determinanty 81 Matice - definice a základní vlastnosti Definice Reálnou resp komplexní maticí A typu m n nazveme obdélníkovou
M Rokyta, MFF UK: Aplikovaná matematika II kap 8: Matice a determinanty 1 8 Matice a determinanty 81 Matice - definice a základní vlastnosti Definice Reálnou resp komplexní maticí A typu m n nazveme obdélníkovou
Lineární algebra : Skalární součin a ortogonalita
 Lineární algebra : Skalární součin a ortogonalita (15. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 30. dubna 2014, 09:00 1 2 15.1 Prehilhertovy prostory Definice 1. Buď V LP nad
Lineární algebra : Skalární součin a ortogonalita (15. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 30. dubna 2014, 09:00 1 2 15.1 Prehilhertovy prostory Definice 1. Buď V LP nad
Matematický ústav Slezské univerzity v Opavě Učební texty k přednášce ALGEBRA II, letní semestr 2000/2001 Michal Marvan. 14.
 Matematický ústav Slezské univerzity v Opavě Učební texty k přednášce ALGEBRA II, letní semestr 2000/2001 Michal Marvan 14. Vlastní vektory Bud V vektorový prostor nad polem P. Lineární zobrazení f : V
Matematický ústav Slezské univerzity v Opavě Učební texty k přednášce ALGEBRA II, letní semestr 2000/2001 Michal Marvan 14. Vlastní vektory Bud V vektorový prostor nad polem P. Lineární zobrazení f : V
CHARAKTERISTICKÉ VEKTORY
 Kapitola 3 CHARAKTERISTICKÉ VEKTORY Nyní se budeme zabývat vlastnostmi matic lineárních zobrazení A: V V, kde V je vektorový prostor dimenze n Protože každý komplexní n -dimenzionální vektorový prostor
Kapitola 3 CHARAKTERISTICKÉ VEKTORY Nyní se budeme zabývat vlastnostmi matic lineárních zobrazení A: V V, kde V je vektorový prostor dimenze n Protože každý komplexní n -dimenzionální vektorový prostor
EUKLIDOVSKÉ PROSTORY
 EUKLIDOVSKÉ PROSTORY Necht L je lineární vektorový prostor nad tělesem reálných čísel R. Zobrazení (.,.) : L L R splňující vlastnosti 1. (x, x) 0 x L, (x, x) = 0 x = 0, 2. (x, y) = (y, x) x, y L, 3. (λx,
EUKLIDOVSKÉ PROSTORY Necht L je lineární vektorový prostor nad tělesem reálných čísel R. Zobrazení (.,.) : L L R splňující vlastnosti 1. (x, x) 0 x L, (x, x) = 0 x = 0, 2. (x, y) = (y, x) x, y L, 3. (λx,
a vlastních vektorů Příklad: Stanovte taková čísla λ, pro která má homogenní soustava Av = λv nenulové (A λ i I) v = 0.
 Výpočet vlastních čísel a vlastních vektorů S pojmem vlastního čísla jsme se již setkali například u iteračních metod pro řešení soustavy lineárních algebraických rovnic. Velikosti vlastních čísel iterační
Výpočet vlastních čísel a vlastních vektorů S pojmem vlastního čísla jsme se již setkali například u iteračních metod pro řešení soustavy lineárních algebraických rovnic. Velikosti vlastních čísel iterační
VĚTY Z LINEÁRNÍ ALGEBRY
 VĚTY Z LINEÁRNÍ ALGEBRY Skripta Matematické metody pro statistiku a operační výzkum (Nešetřilová, H., Šařecová, P., 2009). 1. věta Nechť M = {x 1, x 2,..., x k } je množina vektorů z vektorového prostoru
VĚTY Z LINEÁRNÍ ALGEBRY Skripta Matematické metody pro statistiku a operační výzkum (Nešetřilová, H., Šařecová, P., 2009). 1. věta Nechť M = {x 1, x 2,..., x k } je množina vektorů z vektorového prostoru
Úlohy nejmenších čtverců
 Úlohy nejmenších čtverců Petr Tichý 7. listopadu 2012 1 Problémy nejmenších čtverců Ax b Řešení Ax = b nemusí existovat, a pokud existuje, nemusí být jednoznačné. Často má smysl hledat x tak, že Ax b.
Úlohy nejmenších čtverců Petr Tichý 7. listopadu 2012 1 Problémy nejmenších čtverců Ax b Řešení Ax = b nemusí existovat, a pokud existuje, nemusí být jednoznačné. Často má smysl hledat x tak, že Ax b.
Soustavy. Terminologie. Dva pohledy na soustavu lin. rovnic. Definice: Necht A = (a i,j ) R m,n je matice, b R m,1 je jednosloupcová.
 [1] Terminologie [2] Soustavy lineárních rovnic vlastnosti množin řešení metody hledání řešení nejednoznačnost zápisu řešení Definice: Necht A = (a i,j ) R m,n je matice, b R m,1 je jednosloupcová matice.
[1] Terminologie [2] Soustavy lineárních rovnic vlastnosti množin řešení metody hledání řešení nejednoznačnost zápisu řešení Definice: Necht A = (a i,j ) R m,n je matice, b R m,1 je jednosloupcová matice.
19. Druhý rozklad lineární transformace
 Matematický ústav Slezské univerzity v Opavě Učební texty k přednášce ALGEBRA II, letní semestr 2000/2001 Michal Marvan Úmluva. Všude P = C. Vpřednášce o vlastních vektorech jsme se seznámili s diagonalizovatelnými
Matematický ústav Slezské univerzity v Opavě Učební texty k přednášce ALGEBRA II, letní semestr 2000/2001 Michal Marvan Úmluva. Všude P = C. Vpřednášce o vlastních vektorech jsme se seznámili s diagonalizovatelnými
Zdrojem většiny příkladů je sbírka úloh 1. cvičení ( ) 2. cvičení ( )
 Příklady řešené na cvičení LA II - LS 1/13 Zdrojem většiny příkladů je sbírka úloh http://kam.mff.cuni.cz/~sbirka/ 1. cvičení (..13) 1. Rozhodněte, které z následujících operací jsou skalárním součinem
Příklady řešené na cvičení LA II - LS 1/13 Zdrojem většiny příkladů je sbírka úloh http://kam.mff.cuni.cz/~sbirka/ 1. cvičení (..13) 1. Rozhodněte, které z následujících operací jsou skalárním součinem
AVDAT Vektory a matice
 AVDAT Vektory a matice Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Vektory x = x 1 x 2. x p y = y 1 y 2. y p Řádkový vektor dostaneme transpozicí sloupcového vektoru x
AVDAT Vektory a matice Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Vektory x = x 1 x 2. x p y = y 1 y 2. y p Řádkový vektor dostaneme transpozicí sloupcového vektoru x
Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6)
![Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6) Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6)](/thumbs/96/128965676.jpg) 1. Lineární diferenciální rovnice řádu n [MA1-18:P1.7] rovnice typu y n) + p n 1 )y n 1) +... + p 1 )y + p 0 )y = q) 6) počáteční podmínky: y 0 ) = y 0 y 0 ) = y 1 y n 1) 0 ) = y n 1. 7) Věta 1.3 : Necht
1. Lineární diferenciální rovnice řádu n [MA1-18:P1.7] rovnice typu y n) + p n 1 )y n 1) +... + p 1 )y + p 0 )y = q) 6) počáteční podmínky: y 0 ) = y 0 y 0 ) = y 1 y n 1) 0 ) = y n 1. 7) Věta 1.3 : Necht
FREDHOLMOVA ALTERNATIVA
 FREDHOLMOVA ALTERNATIVA Pavel Jirásek 1 Abstrakt. V tomto článku se snažíme shrnout dosavadní výsledky týkající se Fredholmovy alternativy (FA). Postupně zmíníme FA na prostorech konečné dimenze, FA pro
FREDHOLMOVA ALTERNATIVA Pavel Jirásek 1 Abstrakt. V tomto článku se snažíme shrnout dosavadní výsledky týkající se Fredholmovy alternativy (FA). Postupně zmíníme FA na prostorech konečné dimenze, FA pro
Součin matice A a čísla α definujeme jako matici αa = (d ij ) typu m n, kde d ij = αa ij pro libovolné indexy i, j.
 Kapitola 3 Počítání s maticemi Matice stejného typu můžeme sčítat a násobit reálným číslem podobně jako vektory téže dimenze. Definice 3.1 Jsou-li A (a ij ) a B (b ij ) dvě matice stejného typu m n, pak
Kapitola 3 Počítání s maticemi Matice stejného typu můžeme sčítat a násobit reálným číslem podobně jako vektory téže dimenze. Definice 3.1 Jsou-li A (a ij ) a B (b ij ) dvě matice stejného typu m n, pak
Lineární algebra : Báze a dimenze
 Lineární algebra : Báze a dimenze (5. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 9. dubna 2014, 13:33 1 2 5.1 Báze lineárního prostoru Definice 1. O množině vektorů M z LP V řekneme,
Lineární algebra : Báze a dimenze (5. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 9. dubna 2014, 13:33 1 2 5.1 Báze lineárního prostoru Definice 1. O množině vektorů M z LP V řekneme,
vyjádřete ve tvaru lineární kombinace čtverců (lineární kombinace druhých mocnin). Rozhodněte o definitnosti kvadratické formy κ(x).
 Řešené příklady z lineární algebry - část 6 Typové příklady s řešením Příklad 6.: Kvadratickou formu κ(x) = x x 6x 6x x + 8x x 8x x vyjádřete ve tvaru lineární kombinace čtverců (lineární kombinace druhých
Řešené příklady z lineární algebry - část 6 Typové příklady s řešením Příklad 6.: Kvadratickou formu κ(x) = x x 6x 6x x + 8x x 8x x vyjádřete ve tvaru lineární kombinace čtverců (lineární kombinace druhých
1 Determinanty a inverzní matice
 Determinanty a inverzní matice Definice Necht A = (a ij ) je matice typu (n, n), n 2 Subdeterminantem A ij matice A příslušným pozici (i, j) nazýváme determinant matice, která vznikne z A vypuštěním i-tého
Determinanty a inverzní matice Definice Necht A = (a ij ) je matice typu (n, n), n 2 Subdeterminantem A ij matice A příslušným pozici (i, j) nazýváme determinant matice, která vznikne z A vypuštěním i-tého
VI. Maticový počet. VI.1. Základní operace s maticemi. Definice. Tabulku
 VI Maticový počet VI1 Základní operace s maticemi Definice Tabulku a 11 a 12 a 1n a 21 a 22 a 2n, a m1 a m2 a mn kde a ij R, i = 1,, m, j = 1,, n, nazýváme maticí typu m n Zkráceně zapisujeme (a ij i=1m
VI Maticový počet VI1 Základní operace s maticemi Definice Tabulku a 11 a 12 a 1n a 21 a 22 a 2n, a m1 a m2 a mn kde a ij R, i = 1,, m, j = 1,, n, nazýváme maticí typu m n Zkráceně zapisujeme (a ij i=1m
2 Vektorové normy. Základy numerické matematiky - NMNM201. Definice 1 (Norma). Norma je funkcionál splňující pro libovolné vektory x a y a pro
 Cvičení 1 Základy numerické matematiky - NMNM201 1 Základní pojmy opakování Definice 1 (Norma). Norma je funkcionál splňující pro libovolné vektory x a y a pro libovolný skalár α C následující podmínky:
Cvičení 1 Základy numerické matematiky - NMNM201 1 Základní pojmy opakování Definice 1 (Norma). Norma je funkcionál splňující pro libovolné vektory x a y a pro libovolný skalár α C následující podmínky:
Kapitola 11: Vektory a matice:
 Kapitola 11: Vektory a matice: Prostor R n R n = {(x 1,, x n ) x i R, i = 1,, n}, n N x = (x 1,, x n ) R n se nazývá vektor x i je i-tá souřadnice vektoru x rovnost vektorů: x = y i = 1,, n : x i = y i
Kapitola 11: Vektory a matice: Prostor R n R n = {(x 1,, x n ) x i R, i = 1,, n}, n N x = (x 1,, x n ) R n se nazývá vektor x i je i-tá souřadnice vektoru x rovnost vektorů: x = y i = 1,, n : x i = y i
1 Řešení soustav lineárních rovnic
 1 Řešení soustav lineárních rovnic 1.1 Lineární rovnice Lineární rovnicí o n neznámých x 1,x 2,..., x n s reálnými koeficienty rozumíme rovnici ve tvaru a 1 x 1 + a 2 x 2 +... + a n x n = b, (1) kde koeficienty
1 Řešení soustav lineárních rovnic 1.1 Lineární rovnice Lineární rovnicí o n neznámých x 1,x 2,..., x n s reálnými koeficienty rozumíme rovnici ve tvaru a 1 x 1 + a 2 x 2 +... + a n x n = b, (1) kde koeficienty
Všechno, co jste kdy chtěli vědět o maticích, ale báli jste se zeptat
 Všechno, co jste kdy chtěli vědět o maticích, ale báli jste se zeptat Čtvercová matice n n, např. může reprezentovat: A = A A 2 A 3 A 2 A 22 A 23 A 3 A 32 A 33 matici koeficientů soustavy n lineárních
Všechno, co jste kdy chtěli vědět o maticích, ale báli jste se zeptat Čtvercová matice n n, např. může reprezentovat: A = A A 2 A 3 A 2 A 22 A 23 A 3 A 32 A 33 matici koeficientů soustavy n lineárních
11. Skalární součin a ortogonalita p. 1/16
 11. Skalární součin a ortogonalita 11. Skalární součin a ortogonalita p. 1/16 11. Skalární součin a ortogonalita p. 2/16 Skalární součin a ortogonalita 1. Definice skalárního součinu 2. Norma vektoru 3.
11. Skalární součin a ortogonalita 11. Skalární součin a ortogonalita p. 1/16 11. Skalární součin a ortogonalita p. 2/16 Skalární součin a ortogonalita 1. Definice skalárního součinu 2. Norma vektoru 3.
1 Vektorové prostory a podprostory
 Pro nahrazení účasti v jednotlivých cvičeních (resp. pro studenty kombinované formy) je dostačující vypracování a odevzdání tučně vyznačených příkladů. 1 Vektorové prostory a podprostory Definujte vektorový
Pro nahrazení účasti v jednotlivých cvičeních (resp. pro studenty kombinované formy) je dostačující vypracování a odevzdání tučně vyznačených příkladů. 1 Vektorové prostory a podprostory Definujte vektorový
Učební texty k státní bakalářské zkoušce Matematika Diferenciální rovnice. študenti MFF 15. augusta 2008
 Učební texty k státní bakalářské zkoušce Matematika Diferenciální rovnice študenti MFF 15. augusta 2008 1 7 Diferenciální rovnice Požadavky Soustavy lineárních diferenciálních rovnic prvního řádu lineární
Učební texty k státní bakalářské zkoušce Matematika Diferenciální rovnice študenti MFF 15. augusta 2008 1 7 Diferenciální rovnice Požadavky Soustavy lineárních diferenciálních rovnic prvního řádu lineární
Soustavy linea rnı ch rovnic
 [1] Soustavy lineárních rovnic vlastnosti množin řešení metody hledání řešení nejednoznačnost zápisu řešení a) soustavy, 10, b) P. Olšák, FEL ČVUT, c) P. Olšák 2010, d) BI-LIN, e) L, f) 2009/2010, g)l.
[1] Soustavy lineárních rovnic vlastnosti množin řešení metody hledání řešení nejednoznačnost zápisu řešení a) soustavy, 10, b) P. Olšák, FEL ČVUT, c) P. Olšák 2010, d) BI-LIN, e) L, f) 2009/2010, g)l.
Matematika 1 MA1. 2 Determinant. 3 Adjungovaná matice. 4 Cramerovo pravidlo. 11. přednáška ( ) Matematika 1 1 / 29
 Matematika 1 11. přednáška MA1 1 Opakování 2 Determinant 3 Adjungovaná matice 4 Cramerovo pravidlo 5 Vlastní čísla a vlastní vektory matic 6 Zkouška; konzultace; výběrová matematika;... 11. přednáška (15.12.2010
Matematika 1 11. přednáška MA1 1 Opakování 2 Determinant 3 Adjungovaná matice 4 Cramerovo pravidlo 5 Vlastní čísla a vlastní vektory matic 6 Zkouška; konzultace; výběrová matematika;... 11. přednáška (15.12.2010
1 Vektorové prostory.
 1 Vektorové prostory DefiniceMnožinu V, jejíž prvky budeme označovat a, b, c, z, budeme nazývat vektorovým prostorem právě tehdy, když budou splněny následující podmínky: 1 Je dáno zobrazení V V V, které
1 Vektorové prostory DefiniceMnožinu V, jejíž prvky budeme označovat a, b, c, z, budeme nazývat vektorovým prostorem právě tehdy, když budou splněny následující podmínky: 1 Je dáno zobrazení V V V, které
Necht tedy máme přirozená čísla n, k pod pojmem systém lineárních rovnic rozumíme rovnice ve tvaru
 2. Systémy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních rovnic s koeficienty z pole reálných případně komplexních čísel. Uvádíme podmínku pro existenci řešení systému lineárních
2. Systémy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních rovnic s koeficienty z pole reálných případně komplexních čísel. Uvádíme podmínku pro existenci řešení systému lineárních
7. Lineární vektorové prostory
 7. Lineární vektorové prostory Tomáš Salač MÚ UK, MFF UK LS 2017/18 Tomáš Salač ( MÚ UK, MFF UK ) 7. Lineární vektorové prostory LS 2017/18 1 / 62 7.1 Definice a příklady Definice 7.1 Množina G s binární
7. Lineární vektorové prostory Tomáš Salač MÚ UK, MFF UK LS 2017/18 Tomáš Salač ( MÚ UK, MFF UK ) 7. Lineární vektorové prostory LS 2017/18 1 / 62 7.1 Definice a příklady Definice 7.1 Množina G s binární
Primitivní funkce a Riemann uv integrál Lineární algebra Taylor uv polynom Extrémy funkcí více prom ˇenných Matematika III Matematika III Program
 Program Primitivní funkce a Riemannův integrál Program Primitivní funkce a Riemannův integrál Lineární algebra Program Primitivní funkce a Riemannův integrál Lineární algebra Taylorův polynom Program Primitivní
Program Primitivní funkce a Riemannův integrál Program Primitivní funkce a Riemannův integrál Lineární algebra Program Primitivní funkce a Riemannův integrál Lineární algebra Taylorův polynom Program Primitivní
Kapitola 11: Vektory a matice 1/19
 Kapitola 11: Vektory a matice 1/19 2/19 Prostor R n R n = {(x 1,..., x n ) x i R, i = 1,..., n}, n N x = (x 1,..., x n ) R n se nazývá vektor x i je i-tá souřadnice vektoru x rovnost vektorů: x = y i =
Kapitola 11: Vektory a matice 1/19 2/19 Prostor R n R n = {(x 1,..., x n ) x i R, i = 1,..., n}, n N x = (x 1,..., x n ) R n se nazývá vektor x i je i-tá souřadnice vektoru x rovnost vektorů: x = y i =
a počtem sloupců druhé matice. Spočítejme součin A.B. Označme matici A.B = M, pro její prvky platí:
 Řešené příklady z lineární algebry - část 1 Typové příklady s řešením Příklady jsou určeny především k zopakování látky před zkouškou, jsou proto řešeny se znalostmi učiva celého semestru. Tento fakt se
Řešené příklady z lineární algebry - část 1 Typové příklady s řešením Příklady jsou určeny především k zopakování látky před zkouškou, jsou proto řešeny se znalostmi učiva celého semestru. Tento fakt se
Báze a dimenze vektorových prostorů
 Báze a dimenze vektorových prostorů Buď (V, +, ) vektorový prostor nad tělesem (T, +, ). Nechť u 1, u 2,..., u n je konečná posloupnost vektorů z V. Existují-li prvky s 1, s 2,..., s n T, z nichž alespoň
Báze a dimenze vektorových prostorů Buď (V, +, ) vektorový prostor nad tělesem (T, +, ). Nechť u 1, u 2,..., u n je konečná posloupnost vektorů z V. Existují-li prvky s 1, s 2,..., s n T, z nichž alespoň
Podobnostní transformace
 Schurova věta 1 Podobnostní transformace a výpočet vlastních čísel Obecný princip: Úloha: Řešíme-li matematickou úlohu, je často velmi vhodné hledat její ekvivalentní formulaci tak, aby se řešení úlohy
Schurova věta 1 Podobnostní transformace a výpočet vlastních čísel Obecný princip: Úloha: Řešíme-li matematickou úlohu, je často velmi vhodné hledat její ekvivalentní formulaci tak, aby se řešení úlohy
Matematika B101MA1, B101MA2
 Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
12. Determinanty. 12. Determinanty p. 1/25
 12. Determinanty 12. Determinanty p. 1/25 12. Determinanty p. 2/25 Determinanty 1. Induktivní definice determinantu 2. Determinant a antisymetrické formy 3. Výpočet hodnoty determinantu 4. Determinant
12. Determinanty 12. Determinanty p. 1/25 12. Determinanty p. 2/25 Determinanty 1. Induktivní definice determinantu 2. Determinant a antisymetrické formy 3. Výpočet hodnoty determinantu 4. Determinant
3 Lineární kombinace vektorů. Lineární závislost a nezávislost
 3 Lineární kombinace vektorů. Lineární závislost a nezávislost vektorů. Obrázek 5: Vektor w je lineární kombinací vektorů u a v. Vektory u, v a w jsou lineárně závislé. Obrázek 6: Vektor q je lineární
3 Lineární kombinace vektorů. Lineární závislost a nezávislost vektorů. Obrázek 5: Vektor w je lineární kombinací vektorů u a v. Vektory u, v a w jsou lineárně závislé. Obrázek 6: Vektor q je lineární
Vektorový prostor. Př.1. R 2 ; R 3 ; R n Dvě operace v R n : u + v = (u 1 + v 1,...u n + v n ), V (E 3 )...množina vektorů v E 3,
 Vektorový prostor Příklady: Př.1. R 2 ; R 3 ; R n...aritmetický n-rozměrný prostor Dvě operace v R n : součet vektorů u = (u 1,...u n ) a v = (v 1,...v n ) je vektor u + v = (u 1 + v 1,...u n + v n ),
Vektorový prostor Příklady: Př.1. R 2 ; R 3 ; R n...aritmetický n-rozměrný prostor Dvě operace v R n : součet vektorů u = (u 1,...u n ) a v = (v 1,...v n ) je vektor u + v = (u 1 + v 1,...u n + v n ),
2. Určete jádro KerL zobrazení L, tj. nalezněte alespoň jednu jeho bázi a určete jeho dimenzi.
 Řešené příklady z lineární algebry - část 3 Typové příklady s řešením Příklad 3.1: Zobrazení L: P 3 R 23 je zobrazení z prostoru P 3 všech polynomů do stupně 3 (včetně nulového polynomu) do prostoru R
Řešené příklady z lineární algebry - část 3 Typové příklady s řešením Příklad 3.1: Zobrazení L: P 3 R 23 je zobrazení z prostoru P 3 všech polynomů do stupně 3 (včetně nulového polynomu) do prostoru R
Vlastní čísla a vlastní vektory
 Vlastní čísla a vlastní vektory 1 Motivace Uvažujme lineární prostor všech vázaných vektorů v rovině, které procházejí počátkem, a lineární zobrazení tohoto prostoru do sebe(lineární transformaci, endomorfismus)
Vlastní čísla a vlastní vektory 1 Motivace Uvažujme lineární prostor všech vázaných vektorů v rovině, které procházejí počátkem, a lineární zobrazení tohoto prostoru do sebe(lineární transformaci, endomorfismus)
Lineární algebra : Lineární zobrazení
 Lineární algebra : Lineární zobrazení (6. přednáška František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 20. května 2014, 22:40 1 2 6.1 Lineární zobrazení Definice 1. Buďte P a Q dva lineární prostory
Lineární algebra : Lineární zobrazení (6. přednáška František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 20. května 2014, 22:40 1 2 6.1 Lineární zobrazení Definice 1. Buďte P a Q dva lineární prostory
Vektory a matice. Obsah. Aplikovaná matematika I. Carl Friedrich Gauss. Základní pojmy a operace
 Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Uspořádanou n-tici reálných čísel nazveme aritmetický vektor (vektor), ā = (a 1, a 2,..., a n ). Čísla a 1, a 2,..., a n se nazývají složky vektoru
 1 1. Lineární algebra 1.1. Lineární závislost a nezávislost vektorů. Hodnost matice Aritmetické vektory Uspořádanou n-tici reálných čísel nazveme aritmetický vektor (vektor), ā = (a 1, a 2,..., a n ).
1 1. Lineární algebra 1.1. Lineární závislost a nezávislost vektorů. Hodnost matice Aritmetické vektory Uspořádanou n-tici reálných čísel nazveme aritmetický vektor (vektor), ā = (a 1, a 2,..., a n ).
a + b + c = 2 b + c = 1 a b = a 1 2a 1 + a a 3 + a 5 + 2a 2 + a 2 + a
 Zadání A. 1. Polynom P (x) má v uspořádané bázi (x 2 + x 1, 2x 2 x 1, x 2 + x + 2) souřadnice (1, 1, 1). Najděte jeho souřadnice vzhledem k uspořádané bázi (x 2 1, x 2 + x 1, x 2 + x). Nejprve si spočítáme
Zadání A. 1. Polynom P (x) má v uspořádané bázi (x 2 + x 1, 2x 2 x 1, x 2 + x + 2) souřadnice (1, 1, 1). Najděte jeho souřadnice vzhledem k uspořádané bázi (x 2 1, x 2 + x 1, x 2 + x). Nejprve si spočítáme
1 Zobrazení 1 ZOBRAZENÍ 1. Zobrazení a algebraické struktury. (a) Ukažte, že zobrazení f : x
 1 ZOBRAZENÍ 1 Zobrazení a algebraické struktury 1 Zobrazení Příklad 1.1. (a) Ukažte, že zobrazení f : x na otevřený interval ( 1, 1). x x +1 je bijekce množiny reálných čísel R (b) Necht a, b R, a < b.
1 ZOBRAZENÍ 1 Zobrazení a algebraické struktury 1 Zobrazení Příklad 1.1. (a) Ukažte, že zobrazení f : x na otevřený interval ( 1, 1). x x +1 je bijekce množiny reálných čísel R (b) Necht a, b R, a < b.
maticeteorie 1. Matice A je typu 2 4, matice B je typu 4 3. Jakých rozměrů musí být matice X, aby se dala provést
 Úlohy k zamyšlení 1. Zdůvodněte, proč třetí řádek Hornerova schématu pro vyhodnocení polynomu p v bodě c obsahuje koeficienty polynomu r, pro který platí p(x) = (x c) r(x) + p(c). 2. Dokažte, že pokud
Úlohy k zamyšlení 1. Zdůvodněte, proč třetí řádek Hornerova schématu pro vyhodnocení polynomu p v bodě c obsahuje koeficienty polynomu r, pro který platí p(x) = (x c) r(x) + p(c). 2. Dokažte, že pokud
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
NALG 001 Lineární algebra a geometrie 1, zimní semestr MFF UK Doba řešení: 3 hodiny
 NALG 001 Lineární algebra a geometrie 1, zimní semestr MFF UK Závěrečná zkouška verze cvičná 9.1.2013 Doba řešení: 3 hodiny Přednášející: L. Barto, J. Tůma Křestní jméno: Příjmení: Instrukce Neotvírejte
NALG 001 Lineární algebra a geometrie 1, zimní semestr MFF UK Závěrečná zkouška verze cvičná 9.1.2013 Doba řešení: 3 hodiny Přednášející: L. Barto, J. Tůma Křestní jméno: Příjmení: Instrukce Neotvírejte
Několik aplikací. Kapitola 12
 Kapitola 12 Několik aplikací Diskrétní a rychlá Fourierova transformace Diskrétní Fourierova transformace spočívá ve změně reprezentace polynomu s koeficienty v nějakém tělese T Obvyklá reprezentace polynomu
Kapitola 12 Několik aplikací Diskrétní a rychlá Fourierova transformace Diskrétní Fourierova transformace spočívá ve změně reprezentace polynomu s koeficienty v nějakém tělese T Obvyklá reprezentace polynomu
2.6. Vlastní čísla a vlastní vektory matice
 26 Cíle V této části se budeme zabývat hledáním čísla λ které je řešením rovnice A x = λ x (1) kde A je matice řádu n Znalost řešení takové rovnice má řadu aplikací nejen v matematice Definice 261 Nechť
26 Cíle V této části se budeme zabývat hledáním čísla λ které je řešením rovnice A x = λ x (1) kde A je matice řádu n Znalost řešení takové rovnice má řadu aplikací nejen v matematice Definice 261 Nechť
Symetrické a kvadratické formy
 Symetrické a kvadratické formy Aplikace: klasifikace kvadrik(r 2 ) a kvadratických ploch(r 3 ), optimalizace(mpi) BI-LIN (Symetrické a kvadratické formy) 1 / 20 V celé přednášce uvažujeme číselné těleso
Symetrické a kvadratické formy Aplikace: klasifikace kvadrik(r 2 ) a kvadratických ploch(r 3 ), optimalizace(mpi) BI-LIN (Symetrické a kvadratické formy) 1 / 20 V celé přednášce uvažujeme číselné těleso
9 Kolmost vektorových podprostorů
 9 Kolmost vektorových podprostorů Od kolmosti dvou vektorů nyní přejdeme ke kolmosti dvou vektorových podprostorů. Budeme se zabývat otázkou, kdy jsou dva vektorové podprostory na sebe kolmé a jak to poznáme.
9 Kolmost vektorových podprostorů Od kolmosti dvou vektorů nyní přejdeme ke kolmosti dvou vektorových podprostorů. Budeme se zabývat otázkou, kdy jsou dva vektorové podprostory na sebe kolmé a jak to poznáme.
1 Báze a dimenze vektorového prostoru 1
 1 Báze a dimenze vektorového prostoru 1 Báze a dimenze vektorového prostoru 1 2 Aritmetické vektorové prostory 7 3 Eukleidovské vektorové prostory 9 Levá vnější operace Definice 5.1 Necht A B. Levou vnější
1 Báze a dimenze vektorového prostoru 1 Báze a dimenze vektorového prostoru 1 2 Aritmetické vektorové prostory 7 3 Eukleidovské vektorové prostory 9 Levá vnější operace Definice 5.1 Necht A B. Levou vnější
(Cramerovo pravidlo, determinanty, inverzní matice)
 KMA/MAT1 Přednáška a cvičení, Lineární algebra 2 Řešení soustav lineárních rovnic se čtvercovou maticí soustavy (Cramerovo pravidlo, determinanty, inverzní matice) 16 a 21 října 2014 V dnešní přednášce
KMA/MAT1 Přednáška a cvičení, Lineární algebra 2 Řešení soustav lineárních rovnic se čtvercovou maticí soustavy (Cramerovo pravidlo, determinanty, inverzní matice) 16 a 21 října 2014 V dnešní přednášce
Matematika (CŽV Kadaň) aneb Úvod do lineární algebry Matice a soustavy rovnic
 Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Lineární algebra. Matice, operace s maticemi
 Lineární algebra Matice, operace s maticemi Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo
Lineární algebra Matice, operace s maticemi Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo
10. Soustavy lineárních rovnic, determinanty, Cramerovo pravidlo
 0. Soustavy lineárních rovnic, determinanty, Cramerovo pravidlo (PEF PaA) Petr Gurka aktualizováno 9. prosince 202 Obsah Základní pojmy. Motivace.................................2 Aritmetický vektorový
0. Soustavy lineárních rovnic, determinanty, Cramerovo pravidlo (PEF PaA) Petr Gurka aktualizováno 9. prosince 202 Obsah Základní pojmy. Motivace.................................2 Aritmetický vektorový
K2 7 E=. 2 1 Snadno zjistíme, že všechny nenulové násobky vektoru( 2, 1) jsou vlastními vektorymatice[ϕ]
![K2 7 E=. 2 1 Snadno zjistíme, že všechny nenulové násobky vektoru( 2, 1) jsou vlastními vektorymatice[ϕ] K2 7 E=. 2 1 Snadno zjistíme, že všechny nenulové násobky vektoru( 2, 1) jsou vlastními vektorymatice[ϕ]](/thumbs/91/105934758.jpg) . Vlastní čísla a vlastní vektory.. Uvažujme endomorfismus ϕ na reálném vektorovém prostoru R s maticí [ϕ] K = vzhledemkekanonickébázi K 6. (a) Najděte všechna vlastní čísla a všechny jim příslušné vlastní
. Vlastní čísla a vlastní vektory.. Uvažujme endomorfismus ϕ na reálném vektorovém prostoru R s maticí [ϕ] K = vzhledemkekanonickébázi K 6. (a) Najděte všechna vlastní čísla a všechny jim příslušné vlastní
1 Polynomiální interpolace
 Polynomiální interpolace. Metoda neurčitých koeficientů Příklad.. Nalezněte polynom p co nejmenšího stupně, pro který platí p() = 0, p(2) =, p( ) = 6. Řešení. Polynom hledáme metodou neurčitých koeficientů,
Polynomiální interpolace. Metoda neurčitých koeficientů Příklad.. Nalezněte polynom p co nejmenšího stupně, pro který platí p() = 0, p(2) =, p( ) = 6. Řešení. Polynom hledáme metodou neurčitých koeficientů,
Lineární algebra Operace s vektory a maticemi
 Lineární algebra Operace s vektory a maticemi Robert Mařík 26. září 2008 Obsah Operace s řádkovými vektory..................... 3 Operace se sloupcovými vektory................... 12 Matice..................................
Lineární algebra Operace s vektory a maticemi Robert Mařík 26. září 2008 Obsah Operace s řádkovými vektory..................... 3 Operace se sloupcovými vektory................... 12 Matice..................................
1 Soustavy lineárních rovnic
 1 Soustavy lineárních rovnic 1.1 Základní pojmy Budeme uvažovat soustavu m lineárních rovnic o n neznámých s koeficienty z tělesa T (potom hovoříme o soustavě m lineárních rovnic o n neznámých nad tělesem
1 Soustavy lineárních rovnic 1.1 Základní pojmy Budeme uvažovat soustavu m lineárních rovnic o n neznámých s koeficienty z tělesa T (potom hovoříme o soustavě m lineárních rovnic o n neznámých nad tělesem
Kolik existuje různých stromů na pevně dané n-prvkové množině vrcholů?
 Kapitola 9 Matice a počet koster Graf (orientovaný i neorientovaný) lze popsat maticí, a to hned několika různými způsoby. Tématem této kapitoly jsou incidenční matice orientovaných grafů a souvislosti
Kapitola 9 Matice a počet koster Graf (orientovaný i neorientovaný) lze popsat maticí, a to hned několika různými způsoby. Tématem této kapitoly jsou incidenční matice orientovaných grafů a souvislosti
Lineární algebra : Skalární součin a ortogonalita
 Lineární algebra : Skalární součin a ortogonalita (15. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
Lineární algebra : Skalární součin a ortogonalita (15. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
Operace s maticemi. 19. února 2018
 Operace s maticemi Přednáška druhá 19. února 2018 Obsah 1 Operace s maticemi 2 Hodnost matice (opakování) 3 Regulární matice 4 Inverzní matice 5 Determinant matice Matice Definice (Matice). Reálná matice
Operace s maticemi Přednáška druhá 19. února 2018 Obsah 1 Operace s maticemi 2 Hodnost matice (opakování) 3 Regulární matice 4 Inverzní matice 5 Determinant matice Matice Definice (Matice). Reálná matice
příkladů do cvičení. V textu se objeví i pár detailů, které jsem nestihl (na které jsem zapomněl) a(b u) = (ab) u, u + ( u) = 0 = ( u) + u.
 Několik řešených příkladů do Matematiky Vektory V tomto textu je spočteno několik ukázkových příkladů které vám snad pomohou při řešení příkladů do cvičení. V textu se objeví i pár detailů které jsem nestihl
Několik řešených příkladů do Matematiky Vektory V tomto textu je spočteno několik ukázkových příkladů které vám snad pomohou při řešení příkladů do cvičení. V textu se objeví i pár detailů které jsem nestihl
P 1 = P 1 1 = P 1, P 1 2 =
 1 Výpočet inverzní matice Věta 1 Necht P U elementární matice vzniklá el úpravou U Pak je P U regulární Důkaz: Protože elementární úprava U je invertovatelná, existuje el úprava U, která vrací změny U
1 Výpočet inverzní matice Věta 1 Necht P U elementární matice vzniklá el úpravou U Pak je P U regulární Důkaz: Protože elementární úprava U je invertovatelná, existuje el úprava U, která vrací změny U
Program SMP pro kombinované studium
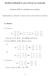 Zadání příkladů k procvičení na seminář Program SMP pro kombinované studium Nejdůležitější typy příkladů - minimum znalostí před zkouškovou písemkou 1) Matice 1. Pro matice 1 0 2 1 0 3 B = 7 3 4 4 2 0
Zadání příkladů k procvičení na seminář Program SMP pro kombinované studium Nejdůležitější typy příkladů - minimum znalostí před zkouškovou písemkou 1) Matice 1. Pro matice 1 0 2 1 0 3 B = 7 3 4 4 2 0
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Vlastní čísla a vlastní vektory
 Kapitola 10 Vlastní čísla a vlastní vektory Základní motivace pro studium vlastních čísel a vektorů pochází z teorie řešení diferenciálních rovnic. Tato teorie říká, že obecné řešení lineární diferenciálnírovnice
Kapitola 10 Vlastní čísla a vlastní vektory Základní motivace pro studium vlastních čísel a vektorů pochází z teorie řešení diferenciálních rovnic. Tato teorie říká, že obecné řešení lineární diferenciálnírovnice
ALGEBRA. Téma 5: Vektorové prostory
 SLEZSKÁ UNIVERZITA V OPAVĚ Matematický ústav v Opavě Na Rybníčku 1, 746 01 Opava, tel. (553) 684 611 DENNÍ STUDIUM Téma 5: Vektorové prostory Základní pojmy Vektorový prostor nad polem P, reálný (komplexní)
SLEZSKÁ UNIVERZITA V OPAVĚ Matematický ústav v Opavě Na Rybníčku 1, 746 01 Opava, tel. (553) 684 611 DENNÍ STUDIUM Téma 5: Vektorové prostory Základní pojmy Vektorový prostor nad polem P, reálný (komplexní)
18. První rozklad lineární transformace
 Matematický ústav Slezské univerzity v Opavě Učební texty k přednášce ALGEBRA II, letní semestr 2000/2001 Michal Marvan 18. První rozklad lineární transformace Úmluva. Vtéto přednášce V je vektorový prostor
Matematický ústav Slezské univerzity v Opavě Učební texty k přednášce ALGEBRA II, letní semestr 2000/2001 Michal Marvan 18. První rozklad lineární transformace Úmluva. Vtéto přednášce V je vektorový prostor
